题目内容
 如图,∠BAD与∠BCD的一边相交于点O,AM、CM分别平分∠BAD和∠BCD,并相交于点M,AM交BC于点E,CM交AD于点F.
如图,∠BAD与∠BCD的一边相交于点O,AM、CM分别平分∠BAD和∠BCD,并相交于点M,AM交BC于点E,CM交AD于点F.(1)若∠B=α,∠D=β,求∠M的度数(用α、β的代数式表示);
(2)若∠B=∠D,ME=MF,求证:AB=CD.
分析:(1)根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系,代入进行计算即可得解;
(2)首先利用(1)中结论得出∠MAF=∠DCF,进而得出△AMF≌△CME,即可得出AE=CF,再求出∠BAE=∠DCF,进而得出△ABE≌△DCF(AAS)即可得出答案.
(2)首先利用(1)中结论得出∠MAF=∠DCF,进而得出△AMF≌△CME,即可得出AE=CF,再求出∠BAE=∠DCF,进而得出△ABE≌△DCF(AAS)即可得出答案.
解答:(1)解:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
所以,∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M,
∴∠M=
(∠B+∠D),
∵∠B=α,∠D=β,
∴∠M=
(α+β);
(2)证明:∵∠B=∠D,∠M=
(∠B+∠D)=∠B=∠D,
∴∠D=∠M,
∵∠AFM=∠DFC,
∴∠MAF=∠DCF,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠ACE=∠DCM=∠MAF,
在△AMF和△CME中 ,
,
,
∴△AMF≌△CME(AAS),
∴AM=CM,
∵EM=MF,
∴AE=CF,
∵∠B=∠D,∠BOA=∠DOC,
∴∠BAO=∠DCO,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAE=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD.
所以,∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M,
∴∠M=
| 1 |
| 2 |
∵∠B=α,∠D=β,
∴∠M=
| 1 |
| 2 |
(2)证明:∵∠B=∠D,∠M=
| 1 |
| 2 |
∴∠D=∠M,
∵∠AFM=∠DFC,
∴∠MAF=∠DCF,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠ACE=∠DCM=∠MAF,
在△AMF和△CME中
 ,
,
|
∴△AMF≌△CME(AAS),
∴AM=CM,
∵EM=MF,
∴AE=CF,
∵∠B=∠D,∠BOA=∠DOC,
∴∠BAO=∠DCO,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAE=∠DCF,
在△ABE和△DCF中,
|
∴△ABE≌△DCF(AAS),
∴AB=CD.
点评:本题考查了三角形的内角和定理,角平分线的定义以及全等三角形的判定与性质等知识,利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.

练习册系列答案
相关题目
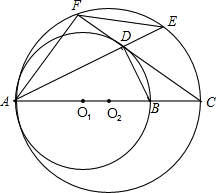 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD. (2012•同安区一模)(1)计算:
(2012•同安区一模)(1)计算: (2013•江西)如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为
(2013•江西)如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为