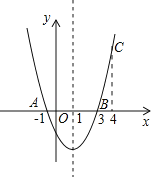题目内容
【题目】二次函数
（
，
，
为常数且
）中的
与
的部分对应值如下表：
| －1 | 0 | 1 | 3 |
| －1 | 3 | 5 | 3 |
给出了结论：
（1）二次函数有最大值，最大值为5；（2）
；（3）
时，的值随值的增大而减小；（4）3是方程
的一个根；（5）当
时，
.则其中正确结论的个数是（ ）
A.4B.3C.2D.1
【答案】B
【解析】
当x=0时，y=3，则c=3；当x=-1时，y=-1；当x=1时，y=5，代入即可求函数解析式y=-x2+3x+3；进而可以进行判断．
解：∵
时
，
时
，
时
.
∴
，
解得：
.
∴
.
当
时，
有最大值，为
，①错误.
，②正确.
∵a=-1<0,开口对称轴为直线，所以，当
时，随
的增大而减小，③错误.
方程为
，解得
，
，所以3是方程
的一个根，④正确.
∵时，
.
∴时，.
∵
时，，且函数有最大值.
∴当
时，
，⑤正确.
综上，正确的有②④⑤，共3个，故选B.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】如图，
是
的直径，
，
为上一动点，过点的直线交于
两点，且
，
于点
，
于点
，当点在上运动时，设
，
（当
的值为0或3时，
的值为2），探究函数随自变量的变化而变化的规律.
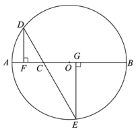
（1）通过取点、画图、测量，得到了x与y的几组对应值，如下表：
| 0 | 0. 40 | 0. 55 | 1. 00 | 1. 80 | 2. 29 | 2. 61 | 3 |
| 2 | 3. 68 | 3. 84 | 3. 65 | 3. 13 | 2. 70 | 2 |
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：点与点
重合时，
长度约为________
（结果保留一位小数）.
