题目内容
4.设$\sqrt{m(x-m)}$+$\sqrt{m(y-m)}$=$\sqrt{x-m}$-$\sqrt{m-y}$在实数范围内成立,其中m,x,y是两两不等的实数,则(x+y)2015的值是( )| A. | 1 | B. | 0 | C. | 2015 | D. | 1或0 |
分析 根据二次根式有意义的条件得到x-m>0,m-y>0,则m≥0且m≤0,所以m=0,于是有$\sqrt{x}$=$\sqrt{-y}$,即x+y=0,然后计算(x+y)2015的值.
解答 解:根据题意得x-m>0,m-y>0,
所以y<m<x,
∵$\sqrt{m(x-m)}$+$\sqrt{m(y-m)}$=$\sqrt{x-m}$-$\sqrt{m-y}$在实数范围内成立,
∴m≥0且m≤0,
∴m=0,
∴$\sqrt{x-m}$-$\sqrt{m-y}$=0,即$\sqrt{x}$=$\sqrt{-y}$
∴x=-y,
即x+y=0,
∴(x+y)2015=0.
故选B.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.也考查了二次根式有意义的条件.

练习册系列答案
相关题目
13.某工程车准备将27根水泥电线杆从公司拉到1km外的公路旁栽立,每隔0.1km栽一根,汽车从公司出发到完成任务后返回到公司称为汽车的总路程,记为y,由于汽车载重量有限,每趟最多只能拉3根水泥杆,为使总路程y尽可能少,汽车除第x趟(x为不大于6的自然数)拉2根外,其余5趟均拉3根,则y与x的函数为( )
| A. | y=0.2x+18.5(1≤x≤6) | B. | y=0.2x+18.7(1≤x≤6) | ||
| C. | y=0.2x+22(1≤x≤6) | D. | y=0.2x+22.2(1≤x≤6) |
13.下列图案是几种名车的标志,请你指出,在这几个图案中是轴对称图形的共有( )
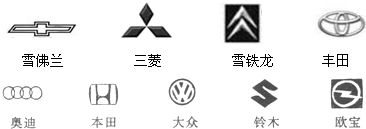

| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |