题目内容
 如图,是五个边长相等的正方形拼成的图形.
如图,是五个边长相等的正方形拼成的图形.
(1)连接DJ,DJ与BE的交点为M,求 的值;
的值;
(2)连接AG,请你判断AG与DJ是否互相垂直,并说明理由.
 解:(1)∵CJ∥DI,
解:(1)∵CJ∥DI,∴∠MBJ=∠MED,∠MJB=∠MDE,
∴△BMJ∽△EMD,
∴
 =
= =2.
=2.(2)AG与DJ互相垂直,设AG与DJ交于Q,
∠MAQ=∠BJM,∠BJM+∠BMQ=90°,
∴∠MAQ+∠BMQ=90°,
∴∠AQD=90°,
∴AG⊥DJ.
分析:(1)要求
 的值,可以使BM,ME成为一对相似三角形的对应边,观察图形,发现证明△BMJ∽△EMD,可以求出
的值,可以使BM,ME成为一对相似三角形的对应边,观察图形,发现证明△BMJ∽△EMD,可以求出 的值.
的值.(2)判断AG与DJ是否互相垂直,即判断∠AQD是否等于90°(设AG与DJ交于Q),∠MAQ+∠AMQ=90°,而∠MAQ=∠BJM,∠BJM+∠BMQ=90°,从而得出结论.
点评:考查了正方形的定义及性质,相似三角形的判定和性质,会用比例求出比值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
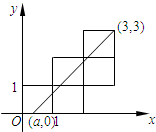 五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是( )
五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图是由五个边长为1的正方形组成的图形,过点A的一条直线和ED,CD分别交于点M,N,假若直线MN在绕点A转动的过程中,存在某一位置,使得直线两侧的图形有相等的面积,则此时PM的长为
如图是由五个边长为1的正方形组成的图形,过点A的一条直线和ED,CD分别交于点M,N,假若直线MN在绕点A转动的过程中,存在某一位置,使得直线两侧的图形有相等的面积,则此时PM的长为 如图,平面直角坐标系中的图案是由五个边长为1的正方形组成的.A(a,0),B(3,3),连接AB的线段将图案的面积分成相等的两部分,则a的值是
如图,平面直角坐标系中的图案是由五个边长为1的正方形组成的.A(a,0),B(3,3),连接AB的线段将图案的面积分成相等的两部分,则a的值是
