题目内容
 如图所示,在矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,则图中全等的直角三角形共有
如图所示,在矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,则图中全等的直角三角形共有
- A.1对
- B.2对
- C.3对
- D.4对
B
分析:先找出图中的直角三角形,再分析三角形全等的方法,然后判断它们之间是否全等.
解答:图中的全等直角三角形有:△ABD≌△CDB,△ADE≌△FCE,
∵四边形ABCD是矩形,
在△ABD和△CDB中,
 ,
,
∴△ABD≌△CDB(SSS).
∵E为CD中点,
∴CE=DE,
在△ADE和△FCE中,
 ,
,
∴△ADE≌△FCE(ASA).
故全等的直角三角形有2对.
故选B.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
分析:先找出图中的直角三角形,再分析三角形全等的方法,然后判断它们之间是否全等.
解答:图中的全等直角三角形有:△ABD≌△CDB,△ADE≌△FCE,
∵四边形ABCD是矩形,
在△ABD和△CDB中,
 ,
,∴△ABD≌△CDB(SSS).
∵E为CD中点,
∴CE=DE,
在△ADE和△FCE中,
 ,
,∴△ADE≌△FCE(ASA).
故全等的直角三角形有2对.
故选B.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
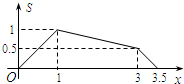
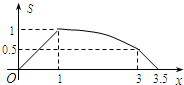
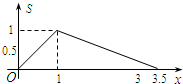
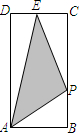 如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )
如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )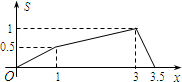
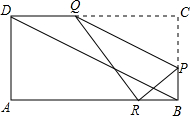
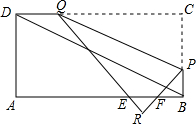
 P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.
P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.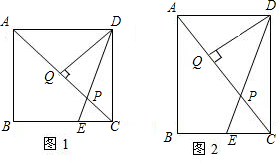 B=nBC
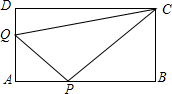
B=nBC 如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.
如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.