��Ŀ����
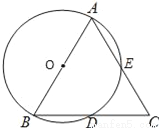
��ͼ����A��B��D��E�ڡ�O�ϣ���AE��BD���ӳ����ཻ�ڵ�C����AB�ǡ�O��ֱ����D��BC���е㣮
��1�����ж�AB��AC֮��Ĵ�С��ϵ��������֤����
��2�����������������£�����ABCΪ��������ʱ����E�Ƿ�AC���е㣿Ϊʲô��
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����A��B��D��E�ڡ�O�ϣ���AE��BD���ӳ����ཻ�ڵ�C����AB�ǡ�O��ֱ����D��BC���е㣮
��1�����ж�AB��AC֮��Ĵ�С��ϵ��������֤����
��2�����������������£�����ABCΪ��������ʱ����E�Ƿ�AC���е㣿Ϊʲô��
