Question

【题目】综合与实践

问题情境

数学活动课上，老师让同学们以“三角形平移与旋转”为主题开展数学活动，和是两个等边三角形纸片，其中，．

解决问题

（1）勤奋小组将和按图1所示的方式摆放(点在同一条直线上) ，连接．发现，请你给予证明；

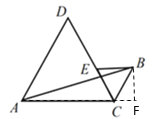
（2）如图2，创新小组在勤奋小组的基础上继续探究，将绕着点逆时针方向旋转，当点恰好落在边上时，求的面积；

拓展延伸

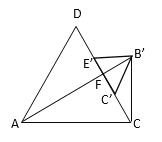
（3）如图3，缜密小组在创新小组的基础上，提出一个问题： “将沿方向平移得到连接，当恰好是以为斜边的直角三角形时，求的值．请你直接写出的值．

Answer 1

【答案】（1）见解析；（2）；（3）2

【解析】

（1）利用SAS证明△ACE≌△DCB即可得到结论；

（2）过点B作BF⊥AC，交AC的延长线于F，求出∠CBF=30°，得到CF=1cm，根据勾股定理求出BF，再根据三角形的面积公式计算即可；

（3）根据∠=90°证得，根据=60°求出，由此得到a的值.

（1）∵和是两个等边三角形，

∴AC=CD，BC=CE，∠ACD=∠ECB=60°，

∴∠ACD+∠DCE=∠ECB+∠DCE,

即∠ACE=∠DCB，

∴△ACE≌△DCB，

∴AE=BD；

（2）由题意得∠ACD=∠ECB=60°，

过点B作BF⊥AC，交AC的延长线于F，

∴∠BCF=180°-∠ACD-∠ECB=60°，∠F=90°，

∴∠CBF=30°，

∴CF=BC=1cm，

∴BF=cm，

∴=；

（3）由题意得∠ACD==60°，

∵∠=90°，

∴,

∵,

∴,

∴=2cm，

∴a=2.