题目内容
3.已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.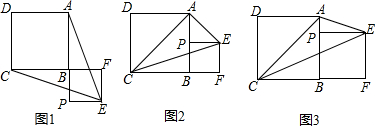
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
分析 (1)根据正方形的性质证明△APE≌△CFE,可得结论;
(2)分别证明∠PAE=45°和∠BAC=45°,则∠CAE=90°,即△ACE是直角三角形;
(3)本题介绍两种解法:
解法一:分别计算PG和BG的长,利用平行线分线段成比例定理列比例式得:$\frac{PE}{BC}=\frac{PG}{GB}$,即$\frac{b}{a}=\frac{a-b}{2b-a}$,
解得:a=$\sqrt{2}$b,得出a与b的比,再计算GH和BG的长,根据角平分线的逆定理得:∠HCG=∠BCG,由平行线的内错角得:∠AEC=∠ACB=45°.
解法二:同理得a与b的比,根据a=$\sqrt{2}$b,BE=$\sqrt{2}$BF,得BE=BC,可得结论.
解答 证明:(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
∵$\left\{\begin{array}{l}{AP=CF}\\{∠P=∠F}\\{PE=EF}\end{array}\right.$,
∴△APE≌△CFE,
∴EA=EC;
(2)△ACE是直角三角形,理由是:
如图2,∵P为AB的中点,
∴PA=PB,
∵PB=PE,
∴PA=PE,
∴∠PAE=45°,
又∵∠BAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
(3)解法一:如图3,设CE交AB于G,
∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a,
∵PE∥CF,
∴$\frac{PE}{BC}=\frac{PG}{GB}$,即$\frac{b}{a}=\frac{a-b}{2b-a}$,
解得:a=$\sqrt{2}$b,
∴a:b=$\sqrt{2}$:1,
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=$\frac{\sqrt{2}}{2}$AG=$\frac{\sqrt{2}}{2}$(2$\sqrt{2}$b-2b)=(2-$\sqrt{2}$)b,
又∵BG=2b-a=(2-$\sqrt{2}$)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
解法二:如图4,连接BE,
易得a=$\sqrt{2}$b,
∴a:b=$\sqrt{2}$:1,
∵BE=$\sqrt{2}$BF=$\sqrt{2}$b,
∴BE=a=BC,
∴∠BCE=∠BEC,
∵∠FBE=∠BCE+∠BEC=45°,
∴∠BCE=22.5°,
∴∠AEC=2∠PEC=2∠BCE=45°.
点评 本题是四边形的综合题,考查了正方形的性质、平行线分线段成比例定理、角平分线的逆定理、等腰直角三角形的性质和判定,前两问难度不大,第三问有难度,作辅助线,设CD=a,PC=b,表示GH和BG的长是关键.

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | -2 | B. | 2 | C. | 0 | D. | -1 |
| A. | 向左平移1个单位 | B. | 向右平移3个单位 | C. | 向上平移3个单位 | D. | 向下平移1个单位 |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
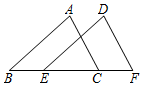 如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )| A. | AC=DF | B. | BE=CF | C. | AC∥DF | D. | ∠A=∠D |
 如图,在?ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}$BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
如图,在?ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}$BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.