题目内容
已知二次函数y=-x2+2ax+1-a,在0≤x≤1时的最小值是-2,求a的值.
考点:二次函数的最值
专题:
分析:把二次函数解析式整理成顶点式形式,然后求出对称轴为直线x=a,再分a<
,和a>
两种情况,利用二次函数的增减性讨论求解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵y=-x2+2ax+1-a=-(x-a)2+a2+1-a,
∴对称轴为直线x=a,
①若a<
,则x=1时取最小值-1+2a+1-a=-2,
解得a=-2,
②若a>
,则x=0时取最小值1-a=-2,
解得a=3,
所以,a的值为-2或3.
∴对称轴为直线x=a,
①若a<
| 1 |
| 2 |
解得a=-2,
②若a>
| 1 |
| 2 |
解得a=3,
所以,a的值为-2或3.
点评:本题考查了二次函数的最值问题,主要利用了二次函数的增减性求最值,难点在于分情况讨论.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
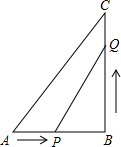 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始向B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P、Q分别从点A,B同时出发,经过多长时间△PBQ的面积等于6cm2?
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始向B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P、Q分别从点A,B同时出发,经过多长时间△PBQ的面积等于6cm2? 如图,A,B,C为圆O上的三等分点.
如图,A,B,C为圆O上的三等分点.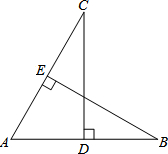 如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E.
如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E.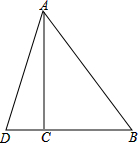 有一块直角三角形绿地ABC,∠ACB=90°,经测量AC=80m,BC=60m,现计划将绿地扩展为以AB为一条边的等腰△ABD,且D点在线段BC的延长线上,求扩展后绿地的面积.
有一块直角三角形绿地ABC,∠ACB=90°,经测量AC=80m,BC=60m,现计划将绿地扩展为以AB为一条边的等腰△ABD,且D点在线段BC的延长线上,求扩展后绿地的面积.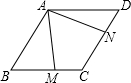 如图,在?ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°,请探索BM,DN与AB的数量关系,并证明你的结论.
如图,在?ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°,请探索BM,DN与AB的数量关系,并证明你的结论. 如图,正方形ABCD中,AC=AF,AF交CD于E,DF∥AC.求证:CF=CE.
如图,正方形ABCD中,AC=AF,AF交CD于E,DF∥AC.求证:CF=CE.