题目内容
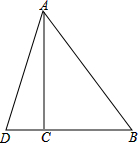 有一块直角三角形绿地ABC,∠ACB=90°,经测量AC=80m,BC=60m,现计划将绿地扩展为以AB为一条边的等腰△ABD,且D点在线段BC的延长线上,求扩展后绿地的面积.
有一块直角三角形绿地ABC,∠ACB=90°,经测量AC=80m,BC=60m,现计划将绿地扩展为以AB为一条边的等腰△ABD,且D点在线段BC的延长线上,求扩展后绿地的面积.考点:勾股定理的应用,等腰三角形的性质
专题:
分析:分以AB为腰和底边两种情况分类讨论即可确定正确的答案.
解答: 解:∵∠ACB=90°,AC=80m,BC=60m,
解:∵∠ACB=90°,AC=80m,BC=60m,
∴AB=
=
=100m,
当以AB为腰,A为顶点时,AB=AD,
扩展后绿地的面积=2S△ABC=60×80=4800m2;
当以AB为腰,B为顶点时,BA=BD,
故DC=DB-BC=40m,
此时扩展后绿地的面积=S△ACD+S△ABC=
×60×80+
×40×80=4000m2;
当以AB为底边时,设DC=x米,
则DC2+AC2=AD2=BD2,
即:x2+802=(x+60)2,
解得:x=
,
此时扩展后绿地的面积=S△ACD+S△ABC=
×60×80+
×
×80=
m2;
 解:∵∠ACB=90°,AC=80m,BC=60m,
解:∵∠ACB=90°,AC=80m,BC=60m,∴AB=
| AC2+AB2 |
| 602+802 |
当以AB为腰,A为顶点时,AB=AD,
扩展后绿地的面积=2S△ABC=60×80=4800m2;
当以AB为腰,B为顶点时,BA=BD,
故DC=DB-BC=40m,
此时扩展后绿地的面积=S△ACD+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
当以AB为底边时,设DC=x米,
则DC2+AC2=AD2=BD2,
即:x2+802=(x+60)2,
解得:x=
| 70 |
| 3 |
此时扩展后绿地的面积=S△ACD+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 70 |
| 3 |
| 10000 |
| 3 |
点评:考查了勾股定理的应用及等腰三角形的性质,能够分类讨论是解决本题的关键,难度中等.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,在△ABC中,BC=2,则中位线DE=
如图,在△ABC中,BC=2,则中位线DE=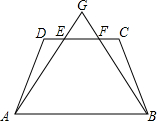 如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.试判断△GAB的形状,并说明理由.
如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.试判断△GAB的形状,并说明理由.