题目内容
2.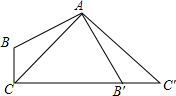 如图,在△ABC中,∠ACB=45°,BC=1,AB=$\sqrt{5}$,将△ABC绕点A逆时针旋转得到△AB′C′,其中点B′与点B是对应点,点C′与点C是对应点,且点C、B′、C′在同一条直线上,则CC′的长为( )
如图,在△ABC中,∠ACB=45°,BC=1,AB=$\sqrt{5}$,将△ABC绕点A逆时针旋转得到△AB′C′,其中点B′与点B是对应点,点C′与点C是对应点,且点C、B′、C′在同一条直线上,则CC′的长为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | 3 |
分析 连接BB′,根据旋转的性质得到AB=AB′,AC=AC′,∠C′=∠ACB=45°,B′C=BC=1,根据等腰三角形的性质得到∠ACC′=∠C=45°,求出∠CAC′=∠BAB′=90°,根据勾股定理得到BB′=$\sqrt{2}$AB=$\sqrt{10}$,CB′=$\sqrt{BB{′}^{2}-B{C}^{2}}$=3,于是得到结论.
解答  解:连接BB′,
解:连接BB′,
∵将△ABC绕点A逆时针旋转得到△AB′C′,
∴AB=AB′,AC=AC′,∠C′=∠ACB=45°,B′C=BC=1,
∴∠ACC′=∠C=45°,
∴∠CAC′=∠BAB′=90°,
∴BB′=$\sqrt{2}$AB=$\sqrt{10}$,
∵∠ACB=∠ACC′=45°,
∴∠BCB′=90°,
∴CB′=$\sqrt{BB{′}^{2}-B{C}^{2}}$=3,
∴CC′=CB′+B′C′=4.
故选A.
点评 本题考查了旋转的性质,直角三角形的性质,等腰三角形的性质,判断出△ABB′是等腰直角三角形是解题关键.

练习册系列答案
相关题目
13.近阶段潍坊持续干旱,给居民生活带来不便,关注水龙头的浪费十分必要,假设20滴水1毫升,一分钟浪费60滴,一年按365天计算,一年浪费水的质量用科学记数法表示为( )克(保留3个有效数字)
| A. | 1.60×106 | B. | 1.57×106 | C. | 1.58×106 | D. | 1.58×105 |
17.已知下列命题
①若|a|=|b|,则a2=b2
②若a>0,b>0,则a+b>0
③到线段两端点距离相等的点在这条线段的垂直平分线上
④矩形的对角线相等
其中原命题与逆命题均为真命题的个数是( )
①若|a|=|b|,则a2=b2
②若a>0,b>0,则a+b>0
③到线段两端点距离相等的点在这条线段的垂直平分线上
④矩形的对角线相等
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.在下列四个选项中,不适合普查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 鞋厂检查生产鞋底能承受的弯折次数 | |
| C. | 学校招聘新教师,对应聘教师面试 | |
| D. | 某中学调查九年级全体540名学生的平均身高 |
14.某种品牌运动服经过两次降价,每件零件售价由640元将为360元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
| A. | 360(1+x)2=640 | B. | 640(1-x)2=360 | C. | 640(1-2x)2=360 | D. | 640(1-x2)=360 |
11.在0,-2,2,-3这四个数中,最小的数是( )
| A. | 0 | B. | -2 | C. | 1 | D. | -3 |
12.一组数据2、9、5、5、8、5、8的中位数是( )
| A. | 2 | B. | 5 | C. | 8 | D. | 9 |
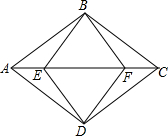 如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.