题目内容
某车间有60人,生产甲乙丙三种零件,每人每小时能生产甲24个,或乙20个,或丙16个.现需用零件甲9个,零件乙15个,零件丙12个装配成某种机件,如何安排劳动力,才能使每小时生产的零件数恰好配成整套?共能生产几套?
考点:三元一次方程组的应用
专题:
分析:可设需要x人生产甲种零件,y人生产乙种零件,z人生产丙种零件,根据等量关系:有60人;需用零件甲9个,零件乙15个,零件丙12个装配成某种机件,列出三元一次方程组,求出方程组的解即可.
解答:解:设需要x人生产甲种零件,y人生产乙种零件,z人生产丙种零件,依题意有
,
解得
,
24x=288,
20y=480,
16z=384,
288÷9=32(套).
答:需要12人生产甲种零件,24人生产乙种零件,24人生产丙种零件,才能使每小时生产的零件数恰好配成整套,共能生产32套.
|
解得
|
24x=288,
20y=480,
16z=384,
288÷9=32(套).
答:需要12人生产甲种零件,24人生产乙种零件,24人生产丙种零件,才能使每小时生产的零件数恰好配成整套,共能生产32套.
点评:考查了三元一次方程组的应用,解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
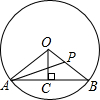 如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上的任意一点,连接AP.若OA=5cm,OC=4cm,则AP的长度可能是
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上的任意一点,连接AP.若OA=5cm,OC=4cm,则AP的长度可能是