题目内容
8.(1)当x何值时,代数式$\frac{x+2}{2}$的值比$\frac{x-1}{3}$的值小2?(2)定义新运算符号“*”的运算过程为a*b=$\frac{1}{2}$a-$\frac{1}{3}$b,试解方程2*(2*x)=1*x.
分析 (1)根据题意列出方程$\frac{x+2}{2}$=$\frac{x-1}{3}$-2,解方程即可;
(2)利用题中的新定义首先得到2*x=1-$\frac{1}{3}$x,那么原方程可化为1-$\frac{1}{3}$(1-$\frac{1}{3}$x)=$\frac{1}{2}$-$\frac{1}{3}$x,求出方程的解即可.
解答 解:(1)根据题意,得$\frac{x+2}{2}$=$\frac{x-1}{3}$-2,
去分母,得3(x+2)=2(x-1)-12,
去括号,得3x+6=2x-2-12,
移项合并,得x=-20;
(2)根据题中的新定义化简2*(2*x)=1*x得:2*(1-$\frac{1}{3}$x)=$\frac{1}{2}$-$\frac{1}{3}$x,
即1-$\frac{1}{3}$(1-$\frac{1}{3}$x)=$\frac{1}{2}$-$\frac{1}{3}$x,
去分母得:6-2(2-$\frac{1}{3}$x)=3-2x,
去括号得:6-4+$\frac{2}{3}$x=3-2x,
去分母得:6+2x=9-6x,
移项合并得:8x=3,
解得:x=$\frac{3}{8}$.
点评 此题考查了一元一次方程的应用及解一元一次方程,根据题意列出方程是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.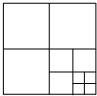 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
(1)将下表填写完整;
(2)an=3n+1(用含n的代数式表示);
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.
 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.(1)将下表填写完整;
| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | an |
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.
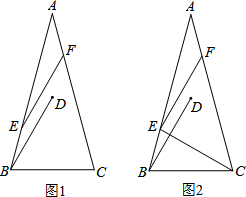 在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.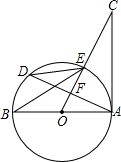 如图,AB是⊙O的直径,AD是弦,OC⊥AD于F,交⊙O于点E,∠BED=∠C.若OA=6,AC=8,则cos∠D=$\frac{2\sqrt{5}}{5}$.
如图,AB是⊙O的直径,AD是弦,OC⊥AD于F,交⊙O于点E,∠BED=∠C.若OA=6,AC=8,则cos∠D=$\frac{2\sqrt{5}}{5}$. 如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.求证:AC∥DF.
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.求证:AC∥DF.