题目内容
20.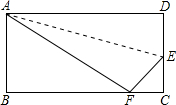 把长AD=10cm,宽AB=6cm的矩形沿着AE对折,使点D落在BC边的点F上,则DE=$\frac{10}{3}$.
把长AD=10cm,宽AB=6cm的矩形沿着AE对折,使点D落在BC边的点F上,则DE=$\frac{10}{3}$.
分析 在△ABF中,利用折叠及勾股定理易得BF长度,即可得CF的长度,用DE表示出EC,利用Rt△EFC的三边关系即可求得DE长度.
解答 解:由折叠的性质知,DE=EF,AF=AD=10cm,
在Rt△ABF中,由勾股定理知,BF=8cm,FC=BC-BF=10-8=2cm,
在Rt△EFC中,由勾股定理知,FC2+CE2=EF2,
(6-DE)2+22=EF2,
解得EF=DE=$\frac{10}{3}$cm.
故答案为:$\frac{10}{3}$,
点评 此题主要考查了折叠的性质、矩形的性质,勾股定理等知识点.利用折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等得出是解题关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
10.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:时刻12:0013:0014:30碑上的数是一个两位数,数字之和为6十位与个位数字与12:00时所看到的正好颠倒了比12:00时看到的两位数中间多了个0则12:00时看到的两位数是( )
| 时刻 | 12:00 | 13:00 | 14:30 |
| 碑上 的数 | 是一个两位数,数字之和为6 | 十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
| A. | 24 | B. | 42 | C. | 51 | D. | 15 |
11.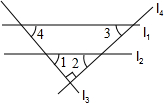 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )| A. | 只有①正确 | B. | 只有②正确 | C. | ①和③正确 | D. | ①②③都正确 |
8. 如图所示,图中的三个矩形中相似的是( )
如图所示,图中的三个矩形中相似的是( )
 如图所示,图中的三个矩形中相似的是( )
如图所示,图中的三个矩形中相似的是( )| A. | 甲、乙和丙 | B. | 甲和乙 | C. | 甲和丙 | D. | 乙和丙 |
15. 一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
 一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{12}$ |
12. 小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )
小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )
 小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )
小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )| A. | (60+x)(40+x)×54%=60×40 | B. | (60+2x)(40+2x)×54%=60×40 | ||
| C. | (60+2x)(40+2x)=60×40×54% | D. | (60+x)(40+x)=60×40×54% |
9.设圆锥侧面展开图的圆心角为n°,母线长为R,底面半径为r.填表:
| n | 60° | 72° | 90° | 120° |
| R关于r的函数解析式 | 6r | 5r | 4r | 3r |
10.在△ABC中,三边长为6、7、x,则x的取值范围是( )
| A. | 2<x<12 | B. | 1<x<13 | C. | 6<x<7 | D. | 无法确定 |
 如图,在矩形ABCD中,E,F为BC上两点,且BE=CF.求证:△ABF≌△DCE.
如图,在矩形ABCD中,E,F为BC上两点,且BE=CF.求证:△ABF≌△DCE.