题目内容
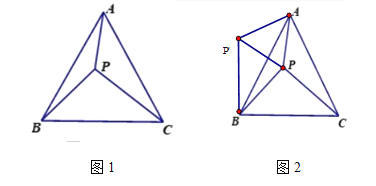
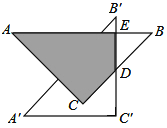
【题目】如图1,菱形![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,把四边形
,把四边形![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .
.


(1)证明:![]() ;
;
(2)求四边形![]() 面积;
面积;
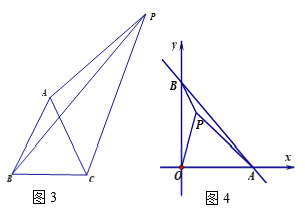
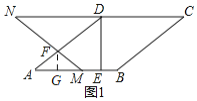
(3)如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路径以每秒
路径以每秒![]() 的速度匀速运动,设运动时间为
的速度匀速运动,设运动时间为![]() 秒,当
秒,当![]() 为何值时,
为何值时,![]() 的面积与四边形
的面积与四边形![]() 的面积相等.
的面积相等.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据平行线的性质和平角的定义,利用同角的补角相等得:![]() ,则
,则![]() ;
;
(2)作![]() 的高线
的高线![]() ,计算
,计算![]() 的长,根据
的长,根据![]() ,计算可得结论;
,计算可得结论;
(3)分两种情况:①![]() 时,如图2,此时
时,如图2,此时![]() 在边
在边![]() 上,②当
上,②当![]() 时,
时,![]() 在
在![]() 上,分别作辅助线,根据
上,分别作辅助线,根据![]() 的面积与四边形
的面积与四边形![]() 的面积相等列等式可得结论.
的面积相等列等式可得结论.
(1)证明:![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() ,
,
由折叠可知![]() ,且
,且![]() ,
,
![]() ,
,
![]() ;
;
(2)解:过点![]() 作
作![]() 于
于![]() ,
,
由(1)可知![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)分两种情况:
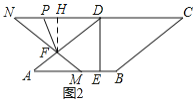
①![]() 时,如图2,此时
时,如图2,此时![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
令![]() 解得:
解得:![]() ;
;
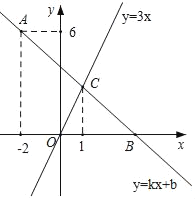
②![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上,如图3,过
上,如图3,过![]() 作
作![]() 于
于![]() ,
,
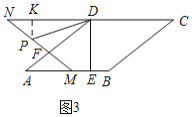
![]() ,
,
![]() ,
,
![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
所以,综上,当![]() 或
或![]() 时,
时,![]() 面积与四边形
面积与四边形![]() 面积相等.
面积相等.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目