Question

【题目】已知，二次函数的图像与x轴的一个交点为O(0,0),点P（m，0）是x轴正半轴上的一个动点.

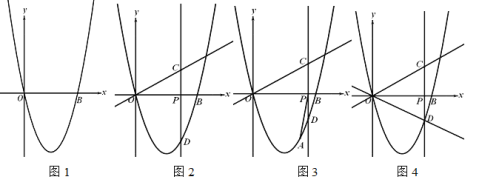
（1）如图1，求二次函数的图像与x轴另一个交点的坐标；

（2）如图2，过点P作x轴的垂线交直线与点C，交二次函数图像于点D，

①当PD=2PC时，求m的值；

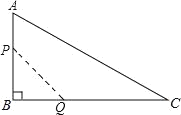
如图3，已知A（3，-3）在二次函数图像上，连结AP，求的最小值；

(3如图4，在第（2）小题的基础上，作直线OD，作点C关于直线OD的对称点C’，当C’落在坐标轴上时，请直接写出m的值.

Answer 1

【答案】（1）二次函数图像与x轴的另一个交点为（4，0）；（2）①当点D在x轴下方时，m= ，当点D在x轴上方时，m= ；②AH=；（3）（点C’在x轴负半轴）（点C’在y轴负半轴）（点C’在x轴正半轴），（点C’在y轴正半轴）

【解析】

（1）将O（0，0）代入，求出解析式再分解得到另一个交点即可.

（2）根据题意，由P（m，0），易得C ，D（m，m2-4m），

①当点D在x轴下方时，，当点D在x轴上方时，分别进行求解.

②过点P作直线OC的垂线，垂足为E，则，所以，

过点A作，AH垂直OC，则AH即为的最小值.

（1）将O（0，0）代入解析式，解得c=0；分从而解析式为y=x2-4x；

因式分解得x2-4x=x（x-4），所以，二次函数图像与x轴的另一个交点为（4，0）

（2）根据题意，由P（m，0），易得C ，D（m，m2-4m），

①当点D在x轴下方时，，解之得，m= ，

当点D在x轴上方时，，解之得，m= ，

②过点P作直线OC的垂线，垂足为E，则，所以，

过点A作，AH垂直OC，则AH即为的最小值。

经计算得AH=，（可用等面积法）

（3）（点C’在x轴负半轴）（点C’在y轴负半轴）

（点C’在x轴正半轴），（点C’在y轴正半轴）