题目内容
 如图1,△ABC中,AB=AC,以AB为直径的⊙O分别与边BC和AC相交于点E和F,过点E作⊙O的切线交边AC于点H.
如图1,△ABC中,AB=AC,以AB为直径的⊙O分别与边BC和AC相交于点E和F,过点E作⊙O的切线交边AC于点H.(1)求证:CH=FH;
(2)如图2,连接OH,若OH=
| 7 |
考点:切线的性质
专题:综合题
分析:(1)连接AE,OE和FE,由AB为圆O的直径,利用直角所对的圆周角为直角得到∠AEB为直角,再由AB=AC,利用三线合一得到BE=CE,根据EH为圆O的切线,利用切线的性质得到EH垂直于OE,得到EH垂直于AC,利用圆内接四边形对角互补及邻补角定义得到∠EFC=∠B,再由∠B=∠C,等量代换得到∠EFC=∠C,利用等角对等边得到EF=EC,利用三线合一即可得证;
(2)过点O作OD⊥AC,可以垂径定理得到D为AF中点,设圆O的半径为r,表示出AF,AD,以及HD,在直角三角形OAD中,表示出OD2,在直角三角形ODH中,利用勾股定理列出关于r的方程,求出方程的解即可得到圆半径r.
(2)过点O作OD⊥AC,可以垂径定理得到D为AF中点,设圆O的半径为r,表示出AF,AD,以及HD,在直角三角形OAD中,表示出OD2,在直角三角形ODH中,利用勾股定理列出关于r的方程,求出方程的解即可得到圆半径r.
解答: (1)证明:连接AE,OE和FE,
(1)证明:连接AE,OE和FE,
∵AB为圆O的直径,
∴∠AEB=90°,
∵AB=AC,
∴BE=EC,
∴OE∥AC,
∵EH为圆O的切线,
∴EH⊥OE,
∴EH⊥AC,
∵∠B+∠AFE=180°,∠EFC+∠AFE=180°,
∴∠B=∠EFC,
∵∠B=∠C,
∴∠EFC=∠C,
∴EF=EC,
∴CH=FH;
(2)解:过点O作OD⊥AC,得到D为AF中点,
设圆O的半径为r,则AF=AC-FC=AB-2CH=2r-2,AD=
=r-1,HD=r-1+1=r,
在Rt△AOD中,根据勾股定理得:OD2=OA2-AD2=r2-(r-1)2,
在Rt△ODH中,根据勾股定理得OD2+DH2=OH2,即r2-(r-1)2+r2=(
)2,
解得:r=-4(舍去)或r=2,
则圆O的半径为2.
 (1)证明:连接AE,OE和FE,
(1)证明:连接AE,OE和FE,∵AB为圆O的直径,
∴∠AEB=90°,
∵AB=AC,
∴BE=EC,
∴OE∥AC,
∵EH为圆O的切线,
∴EH⊥OE,
∴EH⊥AC,
∵∠B+∠AFE=180°,∠EFC+∠AFE=180°,
∴∠B=∠EFC,
∵∠B=∠C,
∴∠EFC=∠C,
∴EF=EC,
∴CH=FH;
(2)解:过点O作OD⊥AC,得到D为AF中点,
设圆O的半径为r,则AF=AC-FC=AB-2CH=2r-2,AD=
| 1 |
| 2 |
在Rt△AOD中,根据勾股定理得:OD2=OA2-AD2=r2-(r-1)2,
在Rt△ODH中,根据勾股定理得OD2+DH2=OH2,即r2-(r-1)2+r2=(
| 7 |
解得:r=-4(舍去)或r=2,
则圆O的半径为2.
点评:此题考查了切线的性质,圆周角定理,等腰三角形的性质,勾股定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
已知点P1(x1,y1),P2(x2,y2),P3(x3,y3)在双曲线y=-
上,且x1<x2<0<x3,则y1,y2,y3的大小关系为( )
| 2 |
| x |
| A、y1<y2<y3 |
| B、y3<y1<y2 |
| C、y2<y3<y1 |
| D、y3>y2>y1 |
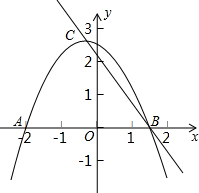 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C,直线y=kx+m(k≠0)经过点C、B,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C,直线y=kx+m(k≠0)经过点C、B,下列结论: 如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE.
如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE.