题目内容
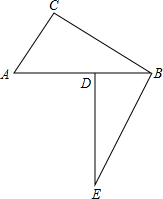 如图:AC⊥BC,ED⊥BD,BE⊥BC,垂足分别为C、D、B,AB=BE,试探究BE与AC+AD之间的关系.
如图:AC⊥BC,ED⊥BD,BE⊥BC,垂足分别为C、D、B,AB=BE,试探究BE与AC+AD之间的关系.考点:全等三角形的判定与性质
专题:
分析:易证△ABC≌△EBD,根据全等三角形对应边相等的性质即可解题.
解答:解:∵ED⊥BD,BE⊥BC,
∴∠DBE+∠CBA=90°,∠DBE+∠E=90°,
∴∠CBA=∠E,
在△ABC和△EBD中,
,
∴△ABC≌△EBD(AAS),
∴AC=BD,
∵AB=AD+BD,
∴BE=AD+AC.
∴∠DBE+∠CBA=90°,∠DBE+∠E=90°,
∴∠CBA=∠E,
在△ABC和△EBD中,
|
∴△ABC≌△EBD(AAS),
∴AC=BD,
∵AB=AD+BD,
∴BE=AD+AC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABC≌△EBD是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某产品进货单价为90元,按100元一件出售时,能售出500件.若每件涨价1元,则销售量就减少10件.则该产品能获得的最大利润为( )
| A、5000元 |
| B、8000元 |
| C、9000元 |
| D、10000元 |
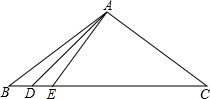 如图,△ABC中,D、E为BC边上的点,且AC⊥AD,∠BAD=∠DAE=12°,AB+AE=BC.求∠C的度数.
如图,△ABC中,D、E为BC边上的点,且AC⊥AD,∠BAD=∠DAE=12°,AB+AE=BC.求∠C的度数.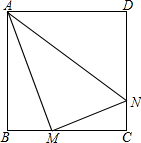 如图,正方形ABCD边长为4cm,M、N分别为BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
如图,正方形ABCD边长为4cm,M、N分别为BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.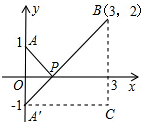 阅读材料:例:说明代数式
阅读材料:例:说明代数式 在梯形ABCD中,AD∥BC,AB⊥BC,AC⊥BD,AC交BD于点O,AD=1,BC=4,求
在梯形ABCD中,AD∥BC,AB⊥BC,AC⊥BD,AC交BD于点O,AD=1,BC=4,求