题目内容
如图，在?ABCD中，E、F分别是AD、BD的中点，若EF=4cm，则CD=考点：三角形中位线定理,平行四边形的性质
专题：
分析：由条件可知EF为△ABD的中位线，可求得AB，结合平行四边形的性质可得AB=CD，可求得答案．
解答：解：∵E、F分别是AD、BD的中点，
∴EF为△ABD的中位线，
∴AB=2EF=8cm，
又∵四边形ABCD为平行四边形，
∴CD=AB=8cm，
故答案为：8．
∴EF为△ABD的中位线，
∴AB=2EF=8cm，
又∵四边形ABCD为平行四边形，
∴CD=AB=8cm，
故答案为：8．
点评：本题主要考查三角形中位线定理，掌握三角形中位线平行且等于第三边的一半是解题的关键．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知：如图，在△ABC中，CD平分∠ACB交AB于点D，∠ADE=∠B，DE交AC于点F．求证：∠EFC=2∠FDC．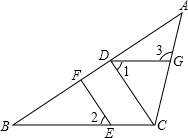
如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．