Question

10．如图，△ABC是以BC为底边的等腰三角形，AB=3，BC=5，P是折线BAC上动点（不与B，C重合），过P作BC的垂线l交BC于D，连接AD．当△ACD是等腰三角形时，BP的长是$\frac{12}{5}$或$\frac{\sqrt{7291}}{25}$．

Answer 1

分析 作AE⊥BC于E，由等腰三角形的性质得出BE=CE=$\frac{1}{2}$BC=$\frac{5}{2}$，分两种情况：①当DC=AC=3时，BD=BC-DC=2，证出PD∥AE，得出△PBD∽BE，得出对应边成比例，即可得出结果；
②当DA=DC时，由等腰三角形的性质得出∠B=∠C=∠DAC，证出△DAC∽△ABC，得出比例式求出DC，得出BD，再证明△PBD∽△ABE，得出对应边成比例，即可得出结果．

解答 解：作AE⊥BC于E，如图所示：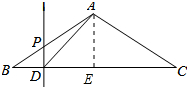
∵AB=AC，
∴BE=CE=$\frac{1}{2}$BC=$\frac{5}{2}$，
分两种情况：
①当DC=AC=3时，BD=BC-DC=5-3=2，
∵PD⊥BC，
∴PD∥AE，
∴△PBD∽△ABE，
∴$\frac{BP}{AB}=\frac{BD}{BE}$，即$\frac{BP}{3}=\frac{2}{\frac{5}{2}}$，
解得：BP=$\frac{12}{5}$；
②当DA=DC时，∠C=∠DAC，
∵AB=AC，
∴∠B=∠C，
∴∠B=∠C=∠DAC，
∴△DAC∽△ABC，
∴$\frac{AC}{BC}=\frac{DC}{AC}$，即$\frac{3}{5}=\frac{DC}{3}$，
解得：DC=$\frac{9}{5}$，
∴BD=BC-DC=5-$\frac{9}{5}$=$\frac{16}{5}$，
∵PD⊥BC，
∴PD∥AE，
∴△PCD∽△ACE，
∴$\frac{PD}{AE}=\frac{DC}{EC}$，即$\frac{PD}{AE}=\frac{\frac{9}{5}}{\frac{5}{2}}$，
解得：PD=$\frac{9\sqrt{11}}{25}$，
∴PB=$\sqrt{B{D}^{2}+P{D}^{2}}$=$\frac{\sqrt{7291}}{25}$；
故答案为：$\frac{12}{5}$或$\frac{\sqrt{7291}}{25}$．

点评 本题考查了等腰三角形的性质、相似三角形的判定与性质；熟练掌握等腰三角形的性质，证明三角形相似得出比例式是解决问题的关键，注意分类讨论．