题目内容
15.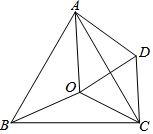 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针旋转60°,得△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针旋转60°,得△ADC,连接OD.(1)判断△COD的形状,并证明;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)直接写出α为多少度时,△AOD是等腰三角形?
分析 (1)由旋转的性质得出CO=CD、∠OCD=60°即可知△COD是等边三角形;
(2)由旋转可以得出 OC=DC,∠DCO=60°,就可以得出△ODC是等边三角形,就可以得出∠ODC=60°,从而得出∠ADO=90°,而得出△AOD的形状;
(3)由条件可以表示出∠AOC=250°-a,就有∠AOD=190°-a,∠ADO=a-60°,当∠DAO=∠DOA,∠AOD=ADO或∠OAD=∠ODA时分别求出a的值即可.
解答 解:(1)△COD是等边三角形,
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,∠OCD=60°
∴CO=CD
∴△COD是等边三角形.
(2)当α=150°时,△AOD是直角三角形.
∵△BOC绕点C按顺时针方向旋转60°得△ADC
∴△BOC≌△ADC,
∴∠BOC=∠ADC=150°
由(1)△COD是等边三角形
∴∠ODC=60°
∴∠ADO=150°-60°=90°
当α=150°时,△AOD是直角三角形.
(3)∵∠AOB=110°,∠BOC=α
∴∠AOC=250°-a.
∵△OCD是等边三角形,
∴∠DOC=∠ODC=60°,
∴∠ADO=a-60°,∠AOD=190°-a,
①当∠DAO=∠DOA时,
2(190°-a)+a-60°=180°,
解得:a=140°
②当∠AOD=ADO时,
190°-a=a-60°,
解得:a=125°,
③当∠OAD=∠ODA时,
190°-a+2(a-60°)=180°,
解得:a=110°
∴α=110°,α=140°,α=125°.
点评 本题考查了等边三角形的判定与性质的运用,旋转的性质的运用,直角三角形的判定,全等三角形的判定及性质的运用,等腰三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
4.下列各式中计算正确的是( )
| A. | $\sqrt{(-4)(-16)}$=$\sqrt{-4}$$•\sqrt{-16}$=(-2)(-4)=8 | B. | $\sqrt{8{a}^{2}}$=4a(a≥0) | ||
| C. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{41+40}$$•\sqrt{41-40}$=9×1=9 | D. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 |
 如图,在平行四边形ABCD中,点E在AD上,BD平分∠EBC.若平行四边形ABCD的周长为10,则△AEB的周长为5.
如图,在平行四边形ABCD中,点E在AD上,BD平分∠EBC.若平行四边形ABCD的周长为10,则△AEB的周长为5. 圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化.
圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化.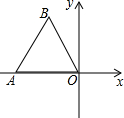 如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).