题目内容
 如图,函数y1=-x+b和函数y2=
如图,函数y1=-x+b和函数y2=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:把M的坐标代入两函数,求出解析式,根据解析式求出N的坐标,即可求出答案.
解答:解:把M(1,4)代入y1=-x+b得:b=5,
即一次函数的解析式是y1=-x+5,
把M(1,4)代入函数y2=
(x>0)得:k=4,
即反比例函数的解析式是y2=
,
把N(n,1)代入y1=-x+5得:n=4,
即N(4,1),
所以当y1<y2时,x的取值范围是x>4或0<x<1,
故答案为:x>4或0<x<1.
即一次函数的解析式是y1=-x+5,
把M(1,4)代入函数y2=
| k |
| x |
即反比例函数的解析式是y2=
| 4 |
| x |
把N(n,1)代入y1=-x+5得:n=4,
即N(4,1),
所以当y1<y2时,x的取值范围是x>4或0<x<1,
故答案为:x>4或0<x<1.
点评:本题考察了一次函数与反比例函数的交点问题,用待定系数法求出反比例函数的解析式的应用,主要考察学生的理解能力和计算能力.

练习册系列答案
相关题目
不等式组
的解集是( )
|
| A、x>2 | B、x>1 |
| C、1<x<2 | D、无解 |

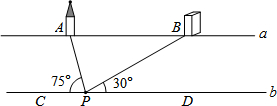
 如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=35°,则∠2=
如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=35°,则∠2=