题目内容
18.若关于x的方程kx2+2x-1=0有实数根,则k的取值范围是k≥-1.分析 由于k的取值不确定,故应分k=0(此时方程化简为一元一次方程)和k≠0(此时方程为二元一次方程)两种情况进行解答.
解答 解:(1)当k=0时,2x-1=0,解得:x=$\frac{1}{2}$;
(2)当k≠0时,此方程是一元二次方程,
∵关于x方程kx2+2x-1=0有实根,
∴△=22-4k×(-1)≥0,解得k≥-1,
由(1)和(2)得,k的取值范围是k≥-1.
故答案为:k≥-1.
点评 本题考查的是根的判别式,注意掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.同时解答此题时要注意分k=0和k≠0两种情况进行讨论.

练习册系列答案
相关题目
6.将一些半径相同的小圆按如图所示的规律摆放: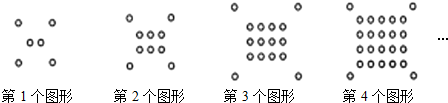
(1)填写下表:
(2)照这样的规律搭下去,搭第8个这样的图形需要76个小圆.

(1)填写下表:
| 图形序号 | 1 | 2 | 3 | 4 | 5 |
| 小圆个数 | 6 | 10 | 16 | 24 | 34 |
10.x10不可能写出如下式子( )
| A. | x2•x4•(x2)2 | B. | (x3)3•x | C. | (-x)3•(-x)5•(-x)2 | D. | (x5)5 |
8.下列运算错误的个数为( )
①(-2)+(-2)=0 ②(-6)+(+4)=-10 ③0+(-3)=(+3)
①(-2)+(-2)=0 ②(-6)+(+4)=-10 ③0+(-3)=(+3)
| A. | 3 个 | B. | 2个 | C. | 1个 | D. | 0个 |
 某地区有一种植物在气温0℃以下持续时间超过2.5小时,即遭霜冻灾害,需采取预防措施,如图是气象台某天发布的该地区气象信息,预报了次日0时至5时气温随时间变化情况,气温是时间的二次函数,它的图象经过点(0,2),其顶点坐标是($\frac{5}{2}$,-$\frac{9}{8}$),请你根据图中信息判断这种植物次日是否需要采取防冻措施?并说明理由.
某地区有一种植物在气温0℃以下持续时间超过2.5小时,即遭霜冻灾害,需采取预防措施,如图是气象台某天发布的该地区气象信息,预报了次日0时至5时气温随时间变化情况,气温是时间的二次函数,它的图象经过点(0,2),其顶点坐标是($\frac{5}{2}$,-$\frac{9}{8}$),请你根据图中信息判断这种植物次日是否需要采取防冻措施?并说明理由. 已知:如图,在△ABC中,∠C=90°,AC=4,CB=5,D是BC边上一点,且DB=2,点E是AC边上的一个动点,过点E作EF∥CB交AD于点F.
已知:如图,在△ABC中,∠C=90°,AC=4,CB=5,D是BC边上一点,且DB=2,点E是AC边上的一个动点,过点E作EF∥CB交AD于点F. 如图,木匠小王想从对角线长为80cm的正方形木板上截下一个最大的洞,试求这个圆的直径是多少?
如图,木匠小王想从对角线长为80cm的正方形木板上截下一个最大的洞,试求这个圆的直径是多少?