题目内容
13.解下列不等式(组),并把它的解集在数轴上表示出来.(1)2(5x-9)≤x+3(4-2x)
(2)$\left\{\begin{array}{l}2x+4≤0\\ \frac{1}{2}(x+8)-2≥0\end{array}\right.$
(3)$\left\{{\begin{array}{l}{\frac{x-2}{7}≥0\;\;\;\;\;\;}\\{-2x-3<1-3x}\end{array}}\right.$
(4)已知方程组$\left\{\begin{array}{l}{x+2y=5a}\\{2x-y=5}\end{array}\right.$的解满足x>0,y<0 化简$|{a+2}|-|{a-\frac{1}{2}}|$.
分析 (1)去括号,然后移项、合并同类项,系数化成1即可求解.
(2)先分别解每个不等式,然后借助数轴确定公共部分即不等式组的解集.
(3)先分别解每个不等式,然后借助数轴确定无公共部分即不等式组无解.
(4)首先解方程组,利用a表示出x,y的值,然后根据x>0,y<0,列不等式组求得a的范围,根据a的范围,以及绝对值的性质即可化简.
解答 解:(1)去括号得:10x-18≤x+12-6x
移项、合并同类项得:15x≤30
系数化为1得:x≤2,
在数轴上表示不等式的解集:
(2)$\left\{\begin{array}{l}{2x+4≤0①}\\{\frac{1}{2}(x+8)-2≥0②}\end{array}\right.$
解不等式①,得x≤-2;
解不等式②,得x≥-4;
因此,原不等式组的解集为-4≤x≤-2,
在数轴上表示不等式的解集: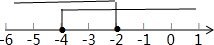
(3)$\left\{\begin{array}{l}{\frac{x-2}{7}≥0①}\\{-2x-3<1-3x②}\end{array}\right.$
由①得,x≥2;
由②得,x<4;
所以不等式的解集为2≤x<4;
在数轴上表示为: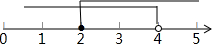
(4)解方程得:$\left\{\begin{array}{l}{x=a+2}\\{y=2a-1}\end{array}\right.$,
∵x>0,y<0,
∴$\left\{\begin{array}{l}{a+2>0}\\{2a-1<0}\end{array}\right.$,
解得:-2<a<$\frac{1}{2}$;
$|{a+2}|-|{a-\frac{1}{2}}|$
=a+2+a-$\frac{1}{2}$
=2a+$\frac{3}{2}$.
点评 本题考查了解一元一次不等式(组),求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了,利用此规律得出不等式的解集是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 听号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 与标准质量的差/g | -10 | +5 | 0 | +5 | 0 | 0 | -5 | 0 | +5 | +10 |
①平均每听罐头的质量是多少?
②这10听罐头的总质量是多少?
| A. | 点P在圆外 | B. | 点P在圆内 | ||
| C. | 点P不在圆上 | D. | 点P在圆外或点P在圆内 |
| A. | ab-4b+3a-12 | B. | ab-4a+3b-12 | C. | ab-4b+3a+12 | D. | ab-4a+3b+12. |
| A. | 4,5,6 | B. | 6,8,10 | C. | 2,3,4 | D. | 1,1,2 |
| A. | m≥1 | B. | m≤1 | C. | m=1 | D. | 一切实数 |
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增减 | +6 | -3 | -2 | +10 | -8 | +18 | -10 |
(2)产量最多的一天比产量最少的一天多生产自行车28辆.
(3)根据记录的数据可知该厂本周实际生产自行车多少辆?
(4)该厂实际每周计件工资制,每生产一辆自行车可得50元,若超额完成任务,则超过部分每辆另奖20元,若未完成任务,则每少生产一辆扣25元,那么该厂工人这一周的工资总额是多少元?
 在Rt△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.问△AEF与△DEB全等吗?说明理由.
在Rt△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.问△AEF与△DEB全等吗?说明理由.