题目内容
5．下列各组数中不可能组成三角形的是（ ）| A． | 5，12，13 | B． | 5，7，12 | C． | 3，4，5 | D． | 101，102，103 |
分析 根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析判断．
解答 解：A中，5+12＞13，13-12＜5，可以构成三角形；
B中，7+5=12，不可以构成三角形；
C中，3+4＞5，5-4＜3，可以构成三角形；
D中，101+102＞103，可以构成三角形．
故选B．
点评 本题主要考查了三角形的三边关系定理：任意两边之和大于第三边，只要满足两短边的和大于最长的边，就可以构成三角形．
练习册系列答案
相关题目
16．数学课上同桌互相出题，小红用?和△遮住“方程组$\left\{\begin{array}{l}{2x+y=?}\\{2x-y=12}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=5}\\{y=△}\end{array}\right.$”中两个数让同桌猜，则?和△这两个数分别为（ ）
| A． | 4和-6 | B． | -6和4 | C． | -2和8 | D． | 8和-2 |
17．如图，自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．
（1）观察图形填写下表：
（2）写出链条的总长度y（cm）与节数n的函数关系；
（3）如果一辆22型的自行车由50节链条环形链接而成，那么这辆自行车的链条链接后的总长度．
（1）观察图形填写下表：
| 链条节数（n） | 2 | 3 | 4 |
| 链条总长度y（cm） | 4.2 | 5.9 | 7.6 |
（3）如果一辆22型的自行车由50节链条环形链接而成，那么这辆自行车的链条链接后的总长度．
如图，在四边形ABCD中，∠B=∠C=60°，BC=1，以CD为直径作圆与AB相切于点M，且交BC边于E点，求BE的长．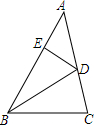
如图，BD是△ABC的角平分线，DE⊥AB，垂足为E，AB=16，BC=12．