题目内容
如图,A、B是第二象限内双曲线y=
 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .


-4
【解析】
试题分析:分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x轴于点E,由于反比例函数的图象在第二象限,所以k<0,由点A是反比例函数图象上的点可知,S△AOD=S△AOF= ,再由A、B两点的横坐标分别是a、2a可知AD=2BE,故点B是AC的二等分点,故DE=a,CE=a,所以S△AOC=S梯形ACOF-S△AOF=6,故可得出k的值.
,再由A、B两点的横坐标分别是a、2a可知AD=2BE,故点B是AC的二等分点,故DE=a,CE=a,所以S△AOC=S梯形ACOF-S△AOF=6,故可得出k的值.
试题解析:分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x轴于点E,


∵反比例函数y= 的图象在
的图象在 第二象限,
第二象限,
∴k<0,
∵点A是反比例函数图象上的点,
∴S△AOD=S△AOF= ,
,
∵A、B两点的横坐标分别是a、2a,
∴AD=2BE,
∴点B是AC的二等分点,
∴DE=a,CE=a,
∴S△AOC=S梯形ACOF-S△AOF=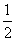 (OE+CE+AF)×OF-
(OE+CE+AF)×OF- =
=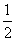 ×4a×
×4a× -
- =6,
=6,
解得k=-4.
【难度】较难

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 = .
= . 的根是 .
的根是 .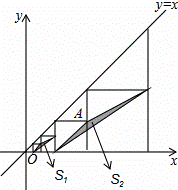
 ,
, ,其中
,其中 为锐角,求证:
为锐角,求证: 。
。

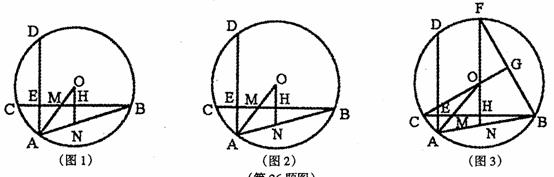 ⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=
⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=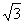 , 求⊙0的半径长.
, 求⊙0的半径长.