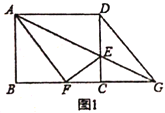
题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,延长
处,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求![]() 的值;
的值;
(2)求证:四边形![]() 是菱形;
是菱形;
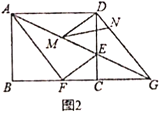
(3)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点(与端点不重合),且
上的动点(与端点不重合),且![]() ,设
,设![]() ,
,![]() ,请解决以下相关问题:
,请解决以下相关问题:
①写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②是否存在这样的点![]() ,使
,使![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见详解;(3)①
;(2)证明见详解;(3)①![]() ,②存在,满足条件的
,②存在,满足条件的![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)由翻折可知:![]() .
.![]() ,设
,设![]() ,则
,则![]() 在
在![]() 中,利用勾股定理构建方程即可EC的长,再求FC的长,再求
中,利用勾股定理构建方程即可EC的长,再求FC的长,再求![]() 的值即可;
的值即可;
(2)先证四边形![]() 是平行四边形,再由AD=AF,即可证得四边形
是平行四边形,再由AD=AF,即可证得四边形![]() 是菱形;
是菱形;
(3)①证明![]() ∽
∽![]() ,可得
,可得![]() ,由此即可解决问题.
,由此即可解决问题.![]() 有两种情形:如图
有两种情形:如图![]() 中,当
中,当![]() 时
时![]() 如图
如图![]() 中,当
中,当![]() 时,作
时,作![]() 于
于![]() 分别求解即可解决问题.
分别求解即可解决问题.
解:(1)如图1中,

∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由翻折可知:![]() .
.![]() ,设
,设![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
在![]() 中,则有:
中,则有:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴EF=DE=5,FC=![]() =4,
=4,
∴![]() =
=![]() =
=![]() ;
;
(2)由翻折可知:∠DAE=∠FAE,AD=AF,
∵![]() ,
,
∴∠DAE=∠FGA,
∴∠FAG=∠FGA,
∴AF=FG,
∴AD=FG,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵AD=AF,
∴四边形![]() 是菱形;
是菱形;
(3)①如图2中,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②存在.有两种情形:如图3-1中,当![]() 时,
时,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3-2中,当![]() 时,作
时,作![]() 于
于![]() .
.

∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解![]() 岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |
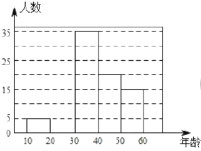
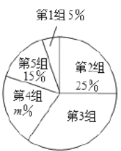
(1)请直接写出![]() 、
、![]() 的值及扇形统计图中第3组所对应的圆心角的度数;
的值及扇形统计图中第3组所对应的圆心角的度数;
(2)请补全上面的频数分布直方图;
(3)假设该市现有![]() 岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?
岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?