题目内容
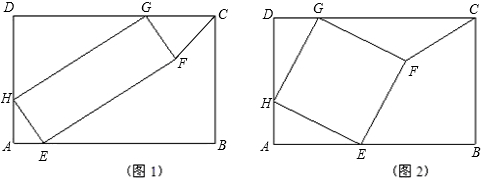
已知,如图1,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.
(1)如图2,当四边形EFGH为正方形时,求CF的长和△FCG的面积;
(2)如图1,设AE=x,三角形FCG的面积=y,求与x之间的函数关系式与y的最大值;
(3)当△CGF是直角三角形时,求x和y值.
(1)如图2,当四边形EFGH为正方形时,求CF的长和△FCG的面积;
(2)如图1,设AE=x,三角形FCG的面积=y,求与x之间的函数关系式与y的最大值;
(3)当△CGF是直角三角形时,求x和y值.

考点:四边形综合题
专题:
分析:(1)要求CF的长和△FCG的面积,需先证△AEH≌△DHG≌△MGF;
(2)先证△AEH∽△DHG,然后根据比例关系,求出y与x之间的函数关系式与y的最大值;
(3)由画图可知∠FGC和∠GCF都不能为直角,当∠GFC=90°时,E、F、C三点在一条直线上,所以△AEH∽△BCE,根据相似三角形的对应线段成比例可求出解.
(2)先证△AEH∽△DHG,然后根据比例关系,求出y与x之间的函数关系式与y的最大值;
(3)由画图可知∠FGC和∠GCF都不能为直角,当∠GFC=90°时,E、F、C三点在一条直线上,所以△AEH∽△BCE,根据相似三角形的对应线段成比例可求出解.
解答:解:(1)(1)作FM⊥CD于M,

可证△AEH≌△DHG≌△MGF,
∴AE=DH=GM=6-2=4,
DG=AH=MF=2,
∴MC=CD-DG-GM=8-2-4=2,
∴FC=
=2
,
∴△FCG的面积=
×6×2=6;
(2)∵△AEH∽△DHG,
∴
=
,即
=
,
∴DG=
,
∴y=△FCG的面积=
×(8-
)×2=8-
,
∵
,
∴1<x≤8,
∴当x=8时,y的最大值为7;
(3)当∠GFC=90°时,E、F、C三点在一条直线上,
∴△AEH∽△BCE
∴
=
,
即
=
,
解得:x=2或x=6.
∴y=4或y=
.
当∠GCF=90°时,此时F点正好落在边BC上,
则△HAE∽△GDH,
=
,
解得:x=4+2
或4-2
,
对应的y=4+2
或4-2
.
当∠CGF=90°时,C,G,H共线,所以不可能.
故x=2,y=4;x=6,y=
;x=4+2
,y=4+2
;x=4-2
,y=4-2
.

可证△AEH≌△DHG≌△MGF,
∴AE=DH=GM=6-2=4,
DG=AH=MF=2,
∴MC=CD-DG-GM=8-2-4=2,
∴FC=
| MF2+MC2 |
| 2 |
∴△FCG的面积=
| 1 |
| 2 |
(2)∵△AEH∽△DHG,
∴
| DG |
| AH |
| GH |
| AE |
| DG |
| 2 |
| 4 |
| x |
∴DG=
| 8 |
| x |
∴y=△FCG的面积=
| 1 |
| 2 |
| 8 |
| x |
| 8 |
| x |
∵
|
∴1<x≤8,
∴当x=8时,y的最大值为7;
(3)当∠GFC=90°时,E、F、C三点在一条直线上,
∴△AEH∽△BCE
∴
| AE |
| BC |
| AH |
| BE |
即
| x |
| 6 |
| 2 |
| 8-x |
解得:x=2或x=6.
∴y=4或y=
| 20 |
| 3 |
当∠GCF=90°时,此时F点正好落在边BC上,
则△HAE∽△GDH,
| HA |
| AE |
| GD |
| DH |
解得:x=4+2
| 2 |
| 2 |
对应的y=4+2
| 2 |
| 2 |
当∠CGF=90°时,C,G,H共线,所以不可能.
故x=2,y=4;x=6,y=
| 20 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了矩形的性质,正方形的性质,以及全等三角形的判定和性质以及相似三角形的判定和性质定理等知识点.综合性强,有一定难度.

练习册系列答案
相关题目
下列四个实数中,最小的数是( )
| A、0.01 | ||
B、-
| ||
| C、-0.1 | ||
| D、-2 |
 如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,
如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD, 如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长,与BC的延长线交于点F,BD=BF.
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长,与BC的延长线交于点F,BD=BF.
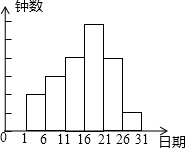 在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题: 小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系. 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.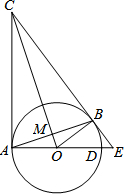 如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB. 如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是
如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是