题目内容
 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.(1)求证:CD是⊙O的切线;
(2)若E是弧AC的中点,⊙O的半径为2,求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:证明题
分析:(1)由OA=OC得∠OCA=∠OAC,由AC平分∠DAB得∠DAC=∠OAC,则∠ADC=∠OCA,根据平行线的判定得OC∥AD,由于AD⊥CD,根据平行线的性质得到OC⊥CD,然后根据切线的判定定理即可得到CD是⊙O的切线;
(2)连结OE,由E是弧AC的中点,根据圆周角定理得∠DAC=∠ECA,而∠DAC=∠OAC,则∠ECA=∠OAC,于是可判断EC∥OA,加上OC∥AE,可判断四边形OAEC为平行四边形,由于OA=OC,则可判断四边形OAEC为菱形,所以CE=OC=OE=2,△OCE都为等边三角形,得到∠COE=∠OCE=60°,易得∠DCE=30°,
在Rt△DCE中,根据含30度的直角三角形三边的关系得DE=1,DC=
,所以S△DCE=
,由于弓形AE的面积=弓形CE的面积,所以S阴影=S△DCE=
(2)连结OE,由E是弧AC的中点,根据圆周角定理得∠DAC=∠ECA,而∠DAC=∠OAC,则∠ECA=∠OAC,于是可判断EC∥OA,加上OC∥AE,可判断四边形OAEC为平行四边形,由于OA=OC,则可判断四边形OAEC为菱形,所以CE=OC=OE=2,△OCE都为等边三角形,得到∠COE=∠OCE=60°,易得∠DCE=30°,
在Rt△DCE中,根据含30度的直角三角形三边的关系得DE=1,DC=
| 3 |
| ||
| 2 |
| ||
| 2 |
解答: (1)证明:∵OA=OC,
(1)证明:∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠ADC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结OE,如图,
∵E是弧AC的中点,
∴∠DAC=∠ECA,
∵∠DAC=∠OAC,
∴∠ECA=∠OAC,
∴EC∥OA,
而OC∥AE,
∴四边形OAEC为平行四边形,
而OA=OC,
∴四边形OAEC为菱形,
∴CE=OC=OE=2,
∴△OCE都为等边三角形,
∴∠COE=∠OCE=60°,
而∠DCO=90°,
∴∠DCE=30°,
在Rt△DCE中,CE=2,
∴DE=
CE=1,DC=
DE=
,
∴S△DCE=
•1•
=
,
∵AE弧=CE弧,
∴弓形AE的面积=弓形CE的面积,
∴S阴影=S△DCE=
.
 (1)证明:∵OA=OC,
(1)证明:∵OA=OC,∴∠OCA=∠OAC,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠ADC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结OE,如图,
∵E是弧AC的中点,
∴∠DAC=∠ECA,
∵∠DAC=∠OAC,
∴∠ECA=∠OAC,
∴EC∥OA,
而OC∥AE,
∴四边形OAEC为平行四边形,
而OA=OC,
∴四边形OAEC为菱形,
∴CE=OC=OE=2,
∴△OCE都为等边三角形,
∴∠COE=∠OCE=60°,
而∠DCO=90°,
∴∠DCE=30°,
在Rt△DCE中,CE=2,
∴DE=
| 1 |
| 2 |
| 3 |
| 3 |
∴S△DCE=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∵AE弧=CE弧,
∴弓形AE的面积=弓形CE的面积,
∴S阴影=S△DCE=
| ||
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了扇形的面积公式.

练习册系列答案
相关题目
 如图,四边形ABCD是正方形,AE、CF分别垂直于过顶点B的直线l,垂足分别为E、F.求证:BE=CF.
如图,四边形ABCD是正方形,AE、CF分别垂直于过顶点B的直线l,垂足分别为E、F.求证:BE=CF.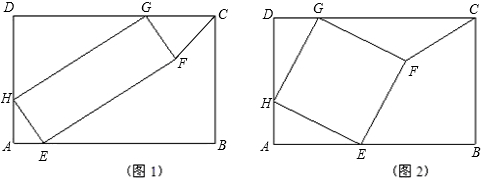

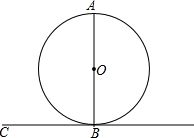 如图,AB是圆O的直径,直线BC与圆O相切于点B.
如图,AB是圆O的直径,直线BC与圆O相切于点B. 如图,△ABC,∠A=70°,点D在BC的延长线上,若∠ACD=130°,则∠B=
如图,△ABC,∠A=70°,点D在BC的延长线上,若∠ACD=130°,则∠B=