题目内容
14.解方程组$\left\{\begin{array}{l}{m-2n=3}\\{3m+5=2n}\end{array}\right.$.分析 根据方程系数的特点,直接用加减消元法解答即可.
解答 解:$\left\{\begin{array}{l}{m-2n=3①}\\{3m+5=2n②}\end{array}\right.$
①-②,得-2m=8,
m=-4
代入②得-12+5=2n,
n=-$\frac{7}{2}$,
所以方程组的解为$\left\{\begin{array}{l}{m=-4}\\{n=-\frac{7}{2}}\end{array}\right.$.
点评 本题考查了解而已一次方程,二元一次方程中,同一未知数的系数相等或互为相反数时,把这两个方程两边相加减,就能消去这个未知数,得到一个一元一次方程.

练习册系列答案
相关题目
6.周长是22cm的等腰三角形,其中一边长为6cm,其它两边长分别为( )
| A. | 6cm,10cm | B. | 8cm,8cm | ||
| C. | 6cm,10cm或8cm,8cm | D. | 无法确定 |


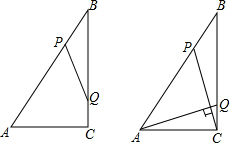 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.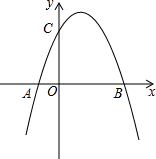 如图,将抛物线y=-x2+1平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),并与x轴交于点C.
如图,将抛物线y=-x2+1平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),并与x轴交于点C.