题目内容
14.在Rt△ABC中,a为直角边,c为斜边,且满足$\sqrt{c-5}$+2$\sqrt{10-2c}$=a-4,求这个三角形的周长和面积.分析 根据二次根式的性质可得c的值,进一步得到a的值,根据勾股定理可求b的值,再根据三角形的周长和面积公式计算即可求解.
解答 解:∵$\sqrt{c-5}$+2$\sqrt{10-2c}$=a-4,
∴c-5=0,
解得c=5,
∴a-4=0,
解得a=4,
∵在Rt△ABC中,a为直角边,c为斜边,
∴b=$\sqrt{{c}^{2}-{a}^{2}}$=3,
∴这个三角形的周长是5+4+3=12,
面积是4×3÷2=6.
点评 考查了二次根式的应用,勾股定理,三角形的周长和面积,关键是根据二次根式的性质可得a、c的值.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
| 等待时间x | 1 | 2 | 5 | 10 | 20 |
| 舒适度指数y | 100 | 50 | 20 | 10 | 5 |
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
19.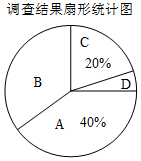 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
请根据以上信息解答下列问题:
(1)参与本次调查的学生共有160人;
(2)统计表中,m=56,n=32;扇形统计图中,B组所对应的圆心角的度数为126°;
(3)若该校共有1500名学生,请估计全校骑自行车上学的学生人数;
(4)该小组据此次调查结果向学校建议扩建学生车棚,若平均每4平方米能停放5辆自行车,请估计在现有300平方米车棚的基础上,至少还需要扩建多少平方米才能满足学生停车需求.
 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:请根据以上信息解答下列问题:
| 组别 | 上学常用的一种交通方式 | 频数(人数) |
| A | 步行 | 64 |
| B | 骑自行车 | m |
| C | 乘公交车 | n |
| D | 其它 | 8 |
(2)统计表中,m=56,n=32;扇形统计图中,B组所对应的圆心角的度数为126°;
(3)若该校共有1500名学生,请估计全校骑自行车上学的学生人数;
(4)该小组据此次调查结果向学校建议扩建学生车棚,若平均每4平方米能停放5辆自行车,请估计在现有300平方米车棚的基础上,至少还需要扩建多少平方米才能满足学生停车需求.
4.某班抽取6名学生参加体能测试,成绩如下:80,90,75,75,80,80,下列表述错误的是( )
| A. | 平均数是80 | B. | 极差是15 | C. | 中位数是80 | D. | 众数是75 |
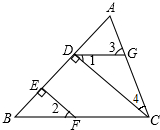 如图,CD⊥AB,EF⊥AB,∠1=∠2,∠ACB=70°,求∠3的度数.
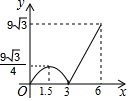
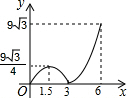
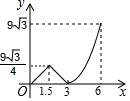
如图,CD⊥AB,EF⊥AB,∠1=∠2,∠ACB=70°,求∠3的度数.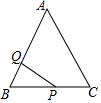 如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )
如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )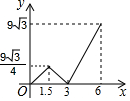
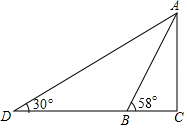 如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)