题目内容
5.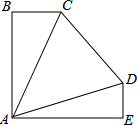 将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.
将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.
分析 延长CB至F,使BF=ED,连接AF,先由SAS证明△ABF≌△AED,得出AF=AD,∠BAF=∠EAD,再证出∠CAD=∠CAF,证明△ACD≌△ACF,得出CD=CF即可.
解答 解:延长CB至F,使BF=ED,连接AF,如图所示: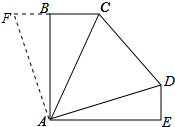 则CF=2+3=5,
则CF=2+3=5,
∵∠ABC=90°,
∴∠ABF=90°,
在△ABF和△AED中,
$\left\{\begin{array}{l}{BF=ED}&{\;}\\{∠ABF=∠E=90°}&{\;}\\{AB=AE}&{\;}\end{array}\right.$,
∴△ABF≌△AED中(SAS),
∴AF=AD,∠BAF=∠EAD,
∵∠BAE=90°,∠CAD=45°,
∴∠BAC+∠EAD=45°,
∴∠BAC+∠BAF=45°,
即∠CAF=45°,
∴∠CAD=∠CAF,
在△ACD和△ACF中,
$\left\{\begin{array}{l}{AF=AD}&{\;}\\{∠CAD=∠CAF}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ACD≌△ACF(SAS),
∴CD=CF=5.
故答案为:5.
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
8.化简$\sqrt{12}$的结果是( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
9.将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为( )
| A. | 1cm | B. | 2cm | C. | 3cm | D. | 4cm |
13.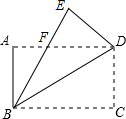 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
(1)求证:△EDF≌△ABF;
(2)∠ABF=30°,AB=2$\sqrt{3}$,求△BDF的面积.
 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.(1)求证:△EDF≌△ABF;
(2)∠ABF=30°,AB=2$\sqrt{3}$,求△BDF的面积.
17.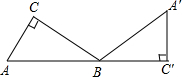 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |
15.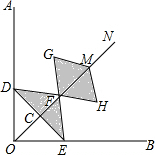 如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
 如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )| A. | y=$\frac{{\sqrt{3}}}{2}{x^2}$ | B. | y=$\sqrt{3}{x^2}$ | C. | y=2$\sqrt{3}{x^2}$ | D. | y=3$\sqrt{3}{x^2}$ |
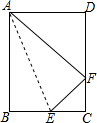 如图,纸片矩形ABCD中,已知:AB=10,AD=8.将AB沿AE折叠,使点B落在边CD的F处,试求:
如图,纸片矩形ABCD中,已知:AB=10,AD=8.将AB沿AE折叠,使点B落在边CD的F处,试求: 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.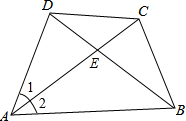 四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.