题目内容
18. 如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O(1)说明∠AOD=∠BOC;
(2)若∠AOC=145°,求∠DOB;
(3)猜想∠AOC+∠DOB的度数,并说明理由.
分析 (1)根据直角三角板可得∠AOB=∠DOC,再利用等式的性质两边同时减去∠BOD可得∠AOD=∠BOC;
(2)首先把∠AOC化为∠AOB+∠BOC,再根据∠AOB=∠DOC=90°可得∴∠AOC+∠BOD=90°+90°=180°,然后再代入∠AOC=145°,可得∠DOB的度数;
(3)证法与(2)相同.
解答 解:(1)∵∠AOB=∠DOC=90°,
∴∠AOB-∠DOB=∠DOC-∠DOB,
∴∠AOD=∠BOC;
(2)∵∠AOB=∠DOC=90°,
∴∠AOC+∠BOD=∠AOB+∠BOC+∠BOD=∠AOB+∠DOC=90°+90°=180°,
∵∠AOC=145°,
∴∠DOB=180°-145°=35°;
(3)∠AOC+∠DOB=180°,
理由:∵∠AOB=∠DOC=90°,
∴∠AOC+∠BOD,
=∠AOB+∠BOC+∠BOD,
=∠AOB+∠DOC,
=90°+90°=180°.
点评 此题主要考查了余角和补角,关键是理清角之间的关系,掌握如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图所示,∠1,∠2,∠A的大小关系是( )
如图所示,∠1,∠2,∠A的大小关系是( )
 如图所示,∠1,∠2,∠A的大小关系是( )
如图所示,∠1,∠2,∠A的大小关系是( )| A. | ∠1>∠2>∠A | B. | ∠1<∠2<∠A | C. | ∠1>∠A>∠2 | D. | ∠2>∠1>∠A |
9. 如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )
如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )
 如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )
如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
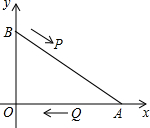 如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题:
如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题: 一个几何体,是由许多规格相同的小正方体堆积而成的,某主视图、俯视图如图所示,要摆成这样的图形至少需用6块正方体,最多需用7块正方体.
一个几何体,是由许多规格相同的小正方体堆积而成的,某主视图、俯视图如图所示,要摆成这样的图形至少需用6块正方体,最多需用7块正方体. 学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.
学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.