题目内容
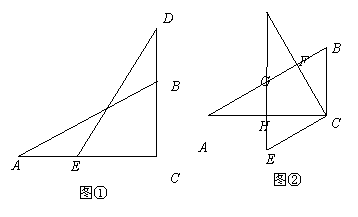
两个大小相同且含 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转 得到图②,点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
得到图②,点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
(1)不添加辅助线,写出图②中所有与△BCF全等的三角形;
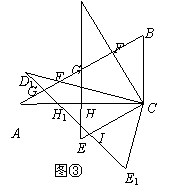
(2)将图②中的△DEC绕点C逆时针旋转 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
(1)图②中与△BCF全等的有△GDF、 △GAH 、△ECH.
(2) =
=
证明:∵ ∴△AF1C ≌△D1H1C.
∴△AF1C ≌△D1H1C.
∴ F1C= H1C, 又CD1=CA,
∴CD1- F1C
="CA-" H1C.即
(3)连结CG1.

在△D1G1F1和△AG1H1中,
∵ ,∴△D1G1F1≌△AG1H1.
,∴△D1G1F1≌△AG1H1.
∴G1F1=G1H1
又∵H1C=F1C,G1C=G1C,∴△CG1F1≌△CG1H1.
∴∠1=∠2.
∵∠B=60°,∠BCF="30°" ,∴∠BFC=90°.
又∵∠DCE=90°,∴∠BFC=∠DCE,
∴BA∥CE, ∴∠1=∠3, ∴∠2=∠3,
∴G1I="CI"
【解析】(1)观察图形,根据全等三角形的判定定理,即可得与△BCF全等的有△GDF、△GAH、△ECH;
(2)利用SAS即可判定△AF1C≌△D1H1C,则可得对应线段相等,即可求得D1F1=AH1;
(3)首先连接CG1,利用AAS即可证得△D1G1F1≌△AG1H1.然后可证得△CG1F1≌△CG1H1.又由平行线的性
质即可求得答案.

 名校课堂系列答案
名校课堂系列答案 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
 (3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
 (3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;