题目内容
规定:sin(-x)=-sinx,cos(-x)=cosx,sin(x+y)=sinx•cosy+cosx•siny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(-60°)=-
;
②sin75°=
;
③sin2x=2sinx•cosx;
④sin(x-y)=sinx•cosy-cosx•siny.
据此判断下列等式成立的是
①cos(-60°)=-
| 1 |
| 2 |
②sin75°=
| ||||
| 4 |
③sin2x=2sinx•cosx;
④sin(x-y)=sinx•cosy-cosx•siny.
考点:锐角三角函数的定义,特殊角的三角函数值
专题:新定义
分析:根据已知中的定义以及特殊角的三角函数值即可判断.
解答:解:①cos(-60°)=cos60°=
,命题错误;
②sin75°=sin(30°+45°)=sin30°•cos45°+cos30°•sin45°=
×
+
×
=
+
=
,命题正确;
③sin2x=sinx•cosx+cosx•sinx=2sinx•cosx,命题正确;
④sin(x-y)=sinx•cos(-y)+cosx•sin(-y)=sinx•cosy-cosx•siny,命题正确.
故答案为:②③④.
| 1 |
| 2 |
②sin75°=sin(30°+45°)=sin30°•cos45°+cos30°•sin45°=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||||
| 4 |
③sin2x=sinx•cosx+cosx•sinx=2sinx•cosx,命题正确;
④sin(x-y)=sinx•cos(-y)+cosx•sin(-y)=sinx•cosy-cosx•siny,命题正确.
故答案为:②③④.
点评:本题考查锐角三角函数以及特殊角的三角函数值,正确理解三角函数的定义是关键.

练习册系列答案
相关题目
 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是



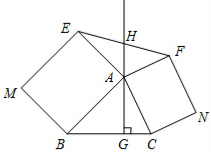 如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.
如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.