题目内容
12.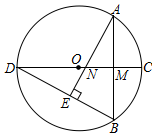 如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC.
如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC.(1)求证:AC=AN
(2)若OM:OC=3:5,AB=5,求⊙O的半径.
分析 (1)连接AC,根据圆周角定理及直角三角形的性质得出∠BDC=∠EAB=∠BAC,再由ASA定理得出△AMN≌△AMC,进而可得出结论;
(2)连接OA,设OM=3x,OC=5x,根据勾股定理求出x的值,进而可得出结论.
解答 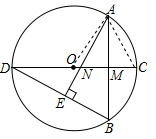 解:(1)连接AC,
解:(1)连接AC,
∵∠AED=∠AMO=90°,
∴∠BDC=∠EAB=∠BAC.
∵AM⊥OC,
∴∠AMC=∠AMN.
在△AMN与△AMC中,
∵$\left\{\begin{array}{l}{∠EAB=∠BAC}\\{AM=AM}\\{∠AMN=∠AMC}\end{array}\right.$,
∴△AMN≌△AMC(ASA),
∴AC=AN;
(2)连接OA,设OM=3x,OC=5x,
∴OA=5x,AM=4x,
∵AB=5,
∴4x=$\frac{5}{2}$,x=$\frac{5}{8}$,
∴r=5x=$\frac{25}{8}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
20.下面三条线段(单位:厘米)可以构成三角形的是( )
| A. | 1、2、3 | B. | 2、3、4 | C. | 5、7、13 | D. | 2、5、8 |
 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3. 如图,AD是△ABC的中线,延长AD至E点,连接BE,要使△ADC≌△EDB,应添加的条件是DE=AD(添加一个条件即可).
如图,AD是△ABC的中线,延长AD至E点,连接BE,要使△ADC≌△EDB,应添加的条件是DE=AD(添加一个条件即可).