题目内容
16.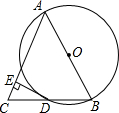 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为E.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为E.(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若DE的长为$\frac{5\sqrt{3}}{2}$,∠BAC=60°,求⊙O的半径.
分析 (1)连接OD、AD,如图,根据圆周角定理由AB为⊙O的直径得∠ADB=90°,再根据等腰三角形的性质得DB=DC;
(2)根据中位线的性质,证得OD∥AC,而DE⊥AC,根据平行线的性质得DE⊥OD,则可根据切线的判定定理得到DE为⊙O的切线;
(3)由∠BAC=60°可判断△ABC为等边三角形,根据等边三角形的性质得∠B=∠C=60°,∠DAC=30°,在RT△AED中,根据正弦函数求得AD,进而在RT△ACD中,根据正弦函数求得AC,即可求得AB,求得半径.
解答 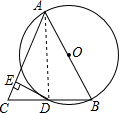 (1)证明:连接OD、AD,如图,
(1)证明:连接OD、AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵△ABC为等腰三角形,
∴DB=DC;
(2)证明:∵OA=OB,DB=DC,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线;
(3)解:∵在等腰△ABC中,∠BAC=60°,
∴△ABC是等边三角形.
∴∠DAC=30°,
∵DE=$\frac{5\sqrt{3}}{2}$,
∴AD=2DE=5$\sqrt{3}$,
∵∠C=60°,
∴sinC=$\frac{AD}{AC}$,
∴AC=$\frac{AD}{sin60°}$=$\frac{5\sqrt{3}}{\frac{\sqrt{3}}{2}}$=10,
∴AB=AC=10,
∴⊙O的半径为5.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了解直角三角形和等腰三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.若关于x的一元二次方程(a+1)x2+x+a2-1=0的一个根是0,则这个方程的另一个根是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
11.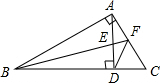 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ①③ |
8.-2011的相反数是( )
| A. | 2011 | B. | -2011 | C. | $\frac{1}{2011}$ | D. | -$\frac{1}{2011}$ |
5.已知代数式$\sqrt{1-x}$+$\sqrt{\frac{1}{x}}$在实数范围内有意义,则x的取值范围是( )
| A. | 0<x≤1 | B. | x≥1 | C. | x>0 | D. | 0≤x≤1 |
6.为了解家里用电量的多少,李明在6月初连续几天同一时刻观察电表显示的读数,并做了如下记录:
由此估计李明家6月份的总用电量是多少?
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 |
| 电表显示(千瓦时) | 117 | 120 | 124 | 129 | 135 | 138 | 142 |
 几何证明.
几何证明. 如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.
如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.