题目内容

3．化简与计算
（1）（-$\frac{a}{b}$）3÷（-ab3）•（-$\frac{{b}^{3}}{a}$）2；    
（2）$\frac{{x}^{2}-4}{{x}^{2}+2x+1}$÷（x+2）•$\frac{x+1}{2-x}$．

分析 （1）先计算乘方、将除法转化为乘法，再约分即可得；
（2）将分子、分母因式分解，同时将除法转化为乘法，再约分即可得．

解答 解：（1）原式=-$\frac{{a}^{3}}{{b}^{3}}$•（-$\frac{1}{a{b}^{3}}$）•$\frac{{b}^{6}}{{a}^{2}}$=1；

（2）原式=-$\frac{（x+2）（x-2）}{（x+1）^{2}}$•$\frac{1}{x+2}$•$\frac{x+1}{x-2}$=-$\frac{1}{x+1}$．

点评 本题主要考查分式的混合运算，熟练掌握分式混合运算顺序和运算法则是解题的关键．

练习册系列答案
相关题目
3．把下列各数填在相应的集合里
+7，$-\frac{3}{5}$，-10，0，0.674，-4，$3\frac{3}{4}$，-9.08，400%，-|-12|
负分数集{$-\frac{3}{5}$，-9.08 }              
正整数集{+7，400%}
整数集 {+7，-10，0，-4，-400%，-|-12| }                
自然数集{+7，0，400% }   
负整数集{-10，-4，-|-12| }               
非负数集{+7，0，0.674，$3\frac{3}{4}$，400% }．
4．如图所示，在△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．求证：
（1）△ABE≌△DCE；
（2）∠ACB=∠DBC．
11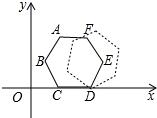．如图的平面直角坐标系中有一个正六边形ABCDEF，其中C、D的坐标分别为（1，0）和（2，0）．若在无滑动的情况下，将这个六边形沿着x轴向右滚动，则在滚动过程中，这个六边形的顶点A、B、C、D、E、F中，会过点（45，2）的是（　　）
A．点AB．点BC．点CD．点D
18．已知整式x+2与x-5的积为x2-3x-10，则一元二次方程x2-3x-10=0的根是（　　）
A．x1=-2，x2=-5B．x1=-2，x2=5C．x1=2，x2=5D．x1=2，x2=-5
8．下列叙述中，正确的有（　　）
①若等腰三角形的两边分别为4和10，则周长为18或24；
②满足条件（$\frac{4}{3}$）2n=（$\frac{3}{4}$）n-3的n不存在；
③任意一个三角形的三条高所在的直线相交于一点，且这点一定在三角形的内部；
④△ABC中，若∠A+∠B=2∠C，∠A-∠C=40°，则这个△ABC为钝角三角形．
A．0个B．1个C．2个D．3个
15．设a、b为任意两个有理数，且ab=|ab|，那么（　　）
A．ab＞0或a=0，或b=0B．ab＞0，或a=0C．a＜0且b＜0D．a，b同号或b=0
12．点A表示-2，在数轴上与点A距离3个单位长度的点表示的数为-5或1．
13．下列各式中正确的是（　　）
A．$\sqrt{9}=±3$B．$\root{3}{-27}=-3$C．$±\sqrt{16}=4$D．$\sqrt{{{（{-2}）}^2}}=-2$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网