题目内容
已知直线y=kx+b在y轴上的截距为4,且经过点C(3,2),直线与x轴,y轴分别相交于A、B,另外在x轴上有一点D(
,0)
(1)求k的值;
(2)求四边形BCDO的面积.
| 3 |
| 2 |
(1)求k的值;
(2)求四边形BCDO的面积.
考点:一次函数图象上点的坐标特征
专题:计算题
分析:(1)把(0,4),(3,2)分别代入y=kx+b得到关于k、b的方程组,然后解方程组即可;
(2)先确定B(0,4),A(6,0),然后利用四边形BCDO的面积=S△ABO-S△CAD进行计算即可.
(2)先确定B(0,4),A(6,0),然后利用四边形BCDO的面积=S△ABO-S△CAD进行计算即可.
解答:
解:(1)把(0,4),(3,2)分别代入y=kx+b得
,解得
,
即k的值为-
;
(2)如图, 直线解析式为y=-
直线解析式为y=-
x+4,
当x=0时,y=-
x+4=4,则B(0,4);当y=0时,-
x+4=0,解得x=6,则A(6,0),
所以四边形BCDO的面积=S△ABO-S△CAD
=
×4×6-
×(6-
)×2
=
.
|
|
即k的值为-
| 2 |
| 3 |
(2)如图,
 直线解析式为y=-
直线解析式为y=-| 2 |
| 3 |
当x=0时,y=-
| 2 |
| 3 |
| 2 |
| 3 |
所以四边形BCDO的面积=S△ABO-S△CAD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=
| 15 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-
,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.
| b |
| k |

练习册系列答案
相关题目
下列计算正确的是( )
| A、a2+a2=a4 |
| B、a2•a3=a6 |
| C、(ab3)2=ab6 |
| D、a3÷a2=a |
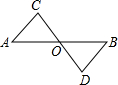 如图,AB与CD相交于点O,且△AOC≌△BOD,有下列结论:
如图,AB与CD相交于点O,且△AOC≌△BOD,有下列结论:(1)AO=BO,(2)AC=BD,(3)O是CD的中点,(4)∠A=∠D,(5)AC∥BD,
其中结论正确的个数是( )
| A、2 | B、3 | C、4 | D、5 |
下列各式变形正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.试猜想线段BC和EF的数量及位置关系,并证明你的猜想.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.试猜想线段BC和EF的数量及位置关系,并证明你的猜想.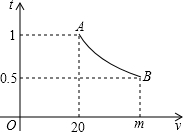 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=