题目内容
 已知:如图,点C为线段AB上的一点,△ACM和△CBN是等边三角形,直线AN、CM交于点E,直线BM、CN交于点F.
已知:如图,点C为线段AB上的一点,△ACM和△CBN是等边三角形,直线AN、CM交于点E,直线BM、CN交于点F.(1)求证:AN=BM;
(2)请你猜想△CEF是什么形状的三角形,并证明你的猜想.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)由等边三角形的性质可得AC=CM,BNC=CN,再利用角的和差可得到∠ACN=BCM,可证明△ACN≌△MCB,可得到AN=BM;
(2)由条件可得∠ECF=60°,结合(1)可得到条件可得∠CAN=∠CBM,可证明△CEN≌△CFB,可得CE=CF,可知△CEF为等边三角形.
(2)由条件可得∠ECF=60°,结合(1)可得到条件可得∠CAN=∠CBM,可证明△CEN≌△CFB,可得CE=CF,可知△CEF为等边三角形.
解答:(1)证明:∵△ACM和△CBN是等边三角形,
∴AC=MC,BC=CN,∠MCA=∠NCB=60°,
∴∠ACN=∠MCB=120°,
在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS),
∴AN=BM;
(2)解:△CEF为等边三角形,证明如下:
∵△ACM和△CBN是等边三角形,
∴∠MCA=∠NCB=60°,
∴∠ECF=180°-60°-60°=60°,
又△ACN≌△MCB,
∴∠ENC=∠FBC,
在△CEN和△CFB中,
,
∴△CEN≌△CFB(ASA),
∴CE=CF,
∴△CEF为等边三角形.
∴AC=MC,BC=CN,∠MCA=∠NCB=60°,
∴∠ACN=∠MCB=120°,
在△ACN和△MCB中,
|
∴△ACN≌△MCB(SAS),
∴AN=BM;
(2)解:△CEF为等边三角形,证明如下:
∵△ACM和△CBN是等边三角形,
∴∠MCA=∠NCB=60°,
∴∠ECF=180°-60°-60°=60°,
又△ACN≌△MCB,
∴∠ENC=∠FBC,
在△CEN和△CFB中,
|
∴△CEN≌△CFB(ASA),
∴CE=CF,
∴△CEF为等边三角形.
点评:本题主要考查全等三角形的判定和性质及等边三角形的性质和判定,掌握全等三角形和等边三角形的判定方法是解题的关键.

练习册系列答案
相关题目
向东走7千米记作+7千米,那么-5千米表示( )
| A、向北走5千米 |
| B、向南走5千米 |
| C、向西走5千米 |
| D、向东走5千米 |
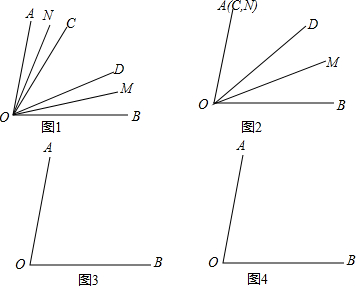 如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC
如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC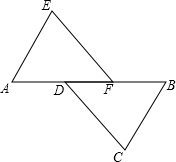 如图,A、D、F、B在同一直线上,AD=BF,EF=CD,且EF∥CD.
如图,A、D、F、B在同一直线上,AD=BF,EF=CD,且EF∥CD.