题目内容
1.解方程或不等式组.(1)-x+3x-4=0.
(2)解不等式组$\left\{\begin{array}{l}\frac{x}{2}>-1\\ 2x+1≥5(x-1)\end{array}\right.$,并写出它的所有所有整数解.
分析 (1)根据解一元一次方程的步骤可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)2x=4
x=2;
(2)由$\frac{x}{2}$>-1,得:x>-2,
由2x+1≥5(x-1),得:x≤2,
所以不等式组的解集为:-2<x≤2
它的整数解为-1、0、1、2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
2.永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
| 日期x | 1 | 2 | 3 | 4 |
| 水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
13.某登山队从大本营出发,在向上攀登的过程中,测得所在位置的气温y℃与向上攀登的高度x km的几组对应值如表:
若每向上攀登1km,所在位置的气温下降幅度基本一致,则向上攀登的海拔高度为2.5km时,登山队所在位置的气温约为-10℃.
| 向上攀登的高度x/km | 0.5 | 1.0 | 1.5 | 2.0 |
| 气温y/℃ | 2.0 | -0.9 | -4.1 | -7.0 |
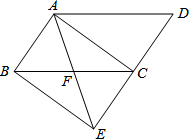 如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.
如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.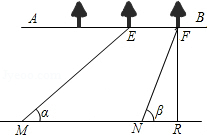 综合实践课,小明所在小组要测量护城河的宽度,如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留整数).
综合实践课,小明所在小组要测量护城河的宽度,如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留整数).