题目内容
14. 如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,p是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,求满足条件的P点坐标.
如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,p是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,求满足条件的P点坐标.
分析 先求出B、O、E的坐标,再根据平行四边形的性质画出图形,即可求出P点的坐标.
解答 解:如图∵△AOE的面积为4,函数y=$\frac{k}{x}$的图象过一、三象限,
∴S△AOE=$\frac{1}{2}$•OE•AE=4,
∴OE•AE=8,
∴xy=8,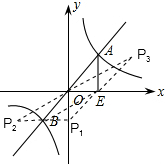 ∴k=8,
∴k=8,
∵函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,
∴2x=$\frac{8}{x}$,
∴x=±2,
当x=2时,y=4,当x=-2时,y=-4,
∴A、B两点的坐标是:(2,4)(-2,-4),
∵以点B、O、E、P为顶点的平行四边形共有3个,
∴满足条件的P点有3个,分别为:
P1(0,-4),P2(-4,-4),P3(4,4).
点评 此题考查了反比例函数综合,用到的知识点是反比例函数的性质、平行四边形的性质,关键是画图形把P点的所有情况都画出来.

练习册系列答案
相关题目
5.不等式2-2x>4的解集是( )
| A. | x<1 | B. | x<-1 | C. | x>3 | D. | x>1 |
19.sin45°-cos60°等于( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{3}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}-\sqrt{3}}{2}$ |
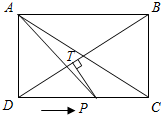 如图,在矩形ABCD中,AD=60cm,CD=80cm,连接AC、BD.动点P从点D出发,以5cm/s速度沿边DC匀速向点C运动,到达点C即停止,过点P作BD的垂线,垂足为T.设点P运动的时间为t s.
如图,在矩形ABCD中,AD=60cm,CD=80cm,连接AC、BD.动点P从点D出发,以5cm/s速度沿边DC匀速向点C运动,到达点C即停止,过点P作BD的垂线,垂足为T.设点P运动的时间为t s.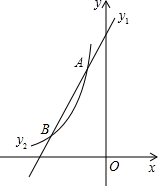 如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.
如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.