题目内容
1.在直角坐标系种中,点P(1,1)(1)点P关于x轴对称的点的坐标是:(1,-1);
(2)点P关于y轴对称的点的坐标是:(-1,1);
(3)点P关于原点对称的点的坐标是:(-1,-1);
(4)将点P绕原点逆时针旋转90°后,得到的点的坐标是:(-1,1);
(5)将点P绕原点顺时针旋转135°后,得到的点的坐标是:(0,-$\sqrt{2}$);
(6)将点P绕另一点M旋转45°得到点Q(1,-1),则M点的坐标为(-$\sqrt{2}$,0),(2+$\sqrt{2}$,0).
分析 (1)、(2)根据关于x轴和y轴对称的点的坐标特征求解;
(3)利用关于原点对称的点的坐标特征求解;
(4)将点P绕原点逆时针旋转90°后得到的点与点P关于y轴对称,与(2)一样求解;
(5)将点P绕原点顺时针旋转135°后得到的点与点P关于x轴对称,与(1)一样求解;
(6)PQ的垂直平分线为x轴,则M点在x轴上,当点P绕另一点M顺时针旋转45°得到点Q,则OM=OP,于是得到此时M(-$\sqrt{2}$,0);当点P绕另一点M逆时针旋转45°得到点Q时,写出点(-$\sqrt{2}$,0)关于直线PQ的对称点即可.
解答 解:(1)点P关于x轴对称的点的坐标是:(1,-1);
(2)点P关于y轴对称的点的坐标是:(-1,1);
(3)点P关于原点对称的点的坐标是:(-1,-1);
(4)将点P绕原点逆时针旋转90°后,得到的点的坐标是:(-1,1);
(5)将点P绕原点顺时针旋转135°后,得到的点的坐标是:(0,-$\sqrt{2}$);
(6)将点P绕另一点M旋转45°得到点Q(1,-1),则M点的坐标为(-$\sqrt{2}$,0),(2+$\sqrt{2}$,0)
故答案为(1,-1),(-1,1),(-1,-1),(-1,1),(0,-$\sqrt{2}$),(-$\sqrt{2}$,0),(2+$\sqrt{2}$,0).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
相关题目
16.下列计算结果等于1的是( )
| A. | (-2)+(-2) | B. | (-2)÷(-2) | C. | -2×(-2) | D. | (-2)-(-2) |
10.流花河上周末的水位为73.1米,下表时本周内水位的变化情况:(“+”表示水位比前一天上升,“-”号表示水位比前一天下降)
(1)试一试,根据上表,请你计算哪天水位最高?
(2)本周日的水位是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化/米 | +0.30 | +0.25 | -0.55 | +0.40 | +0.20 | -0.55 | +0.05 |
(2)本周日的水位是多少?
11.以下列各组线段为边,能组成三角形的是( )
| A. | 2,3,5 | B. | 6,6,6 | C. | 1,1,3 | D. | 3,4,7 |
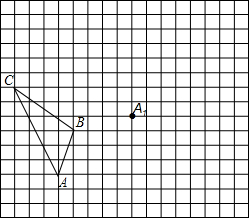 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.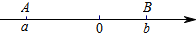 阅读材料:我们知道,若点A、B在数轴上分别表示 有理数a、b(如图所示),A、B两点间的距离表示为AB,则AB=|a-b|.所以式子|x-2|的几何意义是数轴上表示x的点与表示2的点之间的距离.根据上述材料,解答下列问题:
阅读材料:我们知道,若点A、B在数轴上分别表示 有理数a、b(如图所示),A、B两点间的距离表示为AB,则AB=|a-b|.所以式子|x-2|的几何意义是数轴上表示x的点与表示2的点之间的距离.根据上述材料,解答下列问题: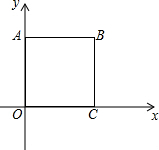 如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:$\sqrt{2}$,点A的坐标为(0,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).
如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:$\sqrt{2}$,点A的坐标为(0,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).