题目内容
4．先化简，再求值：[（x-2y）2+（x-3y）（x+3y）+5y2（1-x）-2x2]÷（-$\frac{1}{2}$xy），其中x=2013，y=-$\frac{1}{2}$．分析 原式中括号中利用完全平方公式，平方差公式，单项式乘以多项式法则计算，合并后利用多项式除以单项式法则计算得到最简结果，把x与y的值代入计算即可求出值．
解答 解：原式=（x2-4xy+4y2+x2-9y2+5y2-5xy2-2x2）÷（-$\frac{1}{2}$xy）=（-4xy-5xy2）÷（-$\frac{1}{2}$xy）=8+10y，
当x=2013，y=-$\frac{1}{2}$时，原式=8-5=3．
点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
15．若式子$\frac{x-3}{\sqrt{x-1}-1}$有意义，则x的取值范围是（ ）
| A． | x≥1且x≠2 | B． | x≥1 | C． | x＞1且x≠2且x≠3 | D． | x＞1且x≠2 |
16．下列语句正确的是（ ）
| A． | 如果一个数的立方根是这个数本身，那么这个数一定是0 | |
| B． | 一个数的立方根不是正数就是负数 | |
| C． | 负数没有立方根 | |
| D． | 一个不为零的数的立方根和这个数同号，0的立方根是0 |
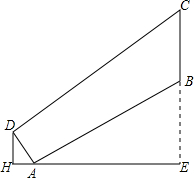如图，在一坡长AB为$70\sqrt{5}$，坡度i1=1：2的山顶B处修建一座铁塔BC，小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°，已知山坡AD的坡度i2=1：0.75
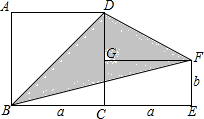如图，正方形ABCD的边长为a，面积为6；长方形CEFG的长、宽分别为a，b，长方形的面积为2，其中点B、C、E在同一直线上，连接DF．求△BDF的面积．