题目内容
若将P(-n,2-n)关于y轴的对称点向下平移1个单位得点P′,则点P′一定不在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:坐标与图形变化-平移,关于x轴、y轴对称的点的坐标
专题:
分析:根据关于y轴对称的点的横坐标是互为相反数,纵坐标相同求出点P关于y轴的对称点,再根据向下平移,横坐标不变,纵坐标减求出点P′的坐标,然后讨论解答即可.
解答:解:P(-n,2-n)关于y轴的对称点为(n,2-n),
∵再向下平移1个单位得到点P′,
∴点P′(n,1-n),
当n<0时,-n>0,
∴1-n>1,
∴点P′(n,1-n)不在第三象限.
故选C.
∵再向下平移1个单位得到点P′,
∴点P′(n,1-n),
当n<0时,-n>0,
∴1-n>1,
∴点P′(n,1-n)不在第三象限.
故选C.
点评:本题考查了坐标与图形变化-平移,关于x轴、y轴对称的点的坐标,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减求出点P′的坐标是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
设
=
-
(A,B为常数),则( )
| 4x-9 |
| 3x2-x-2 |
| A |
| 3x+2 |
| B |
| x-1 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
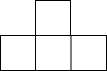
 从不同方向观察同一物体时,可能看到不同的图形.其中,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.请问,下面哪一幅图是右面这个几何体的左视图?( )
从不同方向观察同一物体时,可能看到不同的图形.其中,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.请问,下面哪一幅图是右面这个几何体的左视图?( )


 如图,AB=AD,BC=DC,E、F在AC上,
如图,AB=AD,BC=DC,E、F在AC上,