题目内容
20.直线y=3x+4与抛物线y=x2的交点坐标(4,16),(-1,1).分析 联立两函数的解析式,所得方程组的解,即为两个函数图象的交点坐标.
解答 解:联立两函数的解析式,可得:
$\left\{\begin{array}{l}{y=3x+4}\\{y={x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=4}\\{y=16}\end{array}\right.$
即直线y=3x+4与抛物线y=x2的交点坐标是(4,16),(-1,1).
故答案为:(4,16),(-1,1).
点评 本题考查的是函数图象交点的求法,函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
12.如果∠A是锐角,且sinA=cosA,那么∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?
如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?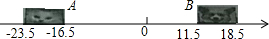 七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题: 如图,点A、B、C、D、E在⊙O上,且$\widehat{AE}$为40°,求∠B+∠D的度数.
如图,点A、B、C、D、E在⊙O上,且$\widehat{AE}$为40°,求∠B+∠D的度数.