题目内容
6.已知二次函数y=mx2+2x+m-4m2的图象经过原点,m=4,这个二次函数的对称轴是x=-$\frac{1}{2}$,开口方向上,顶点坐标(-$\frac{1}{2}$,-1),y的最小值是-1.分析 把原点代入解析式可得到关于m的方程,可求得m的值,则可得到抛物线解析式,化为顶点式,可求得答案.
解答 解:
∵二次函数y=mx2+2x+m-4m2的图象经过原点,
∴m-4m2=0且m≠0,解得m=4,
此时抛物线解析式为y=4x2+2x=4(x+$\frac{1}{2}$)2-1,
∴抛物线对称轴为x=-$\frac{1}{2}$,开口向上,顶点坐标为(-$\frac{1}{2}$,-1),y的最小值是-1,
故答案为:4;x=-$\frac{1}{2}$;上;(-$\frac{1}{2}$,-1);小;-1.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
相关题目
18.若a,b,c,d是四个不同的有理数,ab<0,a-b>0,a+b<0且b+c=0,cd=-1,其中|a|>1,试写出一组符合条件的a,b,c,d,由此你能得到判断a,b,c,d大小关系的方法吗?
16.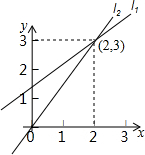 如图,以两条直线l1,l2的交点坐标为解的方程组是( )
如图,以两条直线l1,l2的交点坐标为解的方程组是( )
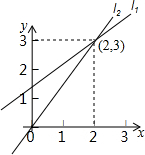 如图,以两条直线l1,l2的交点坐标为解的方程组是( )
如图,以两条直线l1,l2的交点坐标为解的方程组是( )| A. | $\left\{\begin{array}{l}3x-4y=6\\ 3x-2y=0\end{array}$ | B. | $\left\{\begin{array}{l}3x-4y=6\\ 3x+2y=0\end{array}$ | ||
| C. | $\left\{\begin{array}{l}3x-4y=-6\\ 3x-2y=0\end{array}$ | D. | $\left\{\begin{array}{l}-3x+4y=6\\ 3x+2y=0\end{array}$ |
 如图,在四边形ABCD中,AD∥BC,点E、F为AB上的两点,且△DAF≌△CBE.
如图,在四边形ABCD中,AD∥BC,点E、F为AB上的两点,且△DAF≌△CBE.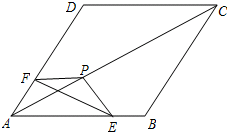 如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.