��Ŀ����
��֪����ƽ��ֱ������ϵxOy�У����κ���y=mx2+2mx-4��m��0����ͼ����x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C����ABC�����Ϊ12��
��1����������κ����Ľ���ʽ��
��2����D������Ϊ��-2��1������P�ڶ��κ�����ͼ���ϣ���ADPΪ��ǣ���tan��ADP=2����ֱ��д����P�ĺ����ꣻ
��3����E��x����������ϣ���OCE��45�㣬��O���O�����EC����ֱ�߶Գƣ�����O��O��E�Ĵ��ߣ�����Ϊ��N��ON��EC���ڵ�M����EM•EC=48�����E�����꣮
��1����������κ����Ľ���ʽ��
��2����D������Ϊ��-2��1������P�ڶ��κ�����ͼ���ϣ���ADPΪ��ǣ���tan��ADP=2����ֱ��д����P�ĺ����ꣻ
��3����E��x����������ϣ���OCE��45�㣬��O���O�����EC����ֱ�߶Գƣ�����O��O��E�Ĵ��ߣ�����Ϊ��N��ON��EC���ڵ�M����EM•EC=48�����E�����꣮
���㣺���κ����ۺ���
ר�⣺
��������1�����ݶԳ������깫ʽ������κ���ͼ��ĶԳ����x=0ʱ��y=-4�������C������Ϊ��0��-4�������������������ʽ����AB=6����һ���õ�A���B�������ֱ�Ϊ��-4��0������2��0��������ϵ����������κ����Ľ���ʽ��
��2����DF��x���ڵ�F�����������������������P��ֱ��AD���·�ʱ������������P��ֱ��AD���Ϸ�ʱ���ӳ�P1A����Gʹ��AG=AP1������DG����GH��x���ڵ�H������������ۿ����P1�����ꣻ
��3������OO�䣬��CE��T������CO�䣮�������Ǻ����������ɵ�OE2=ET•EC=48+TM•EC��ͬ��OC2=CT•EC=TM•EC=16���õ�OE=8���Ӷ��õ���E�����꣮
��2����DF��x���ڵ�F�����������������������P��ֱ��AD���·�ʱ������������P��ֱ��AD���Ϸ�ʱ���ӳ�P1A����Gʹ��AG=AP1������DG����GH��x���ڵ�H������������ۿ����P1�����ꣻ
��3������OO�䣬��CE��T������CO�䣮�������Ǻ����������ɵ�OE2=ET•EC=48+TM•EC��ͬ��OC2=CT•EC=TM•EC=16���õ�OE=8���Ӷ��õ���E�����꣮
��� �⣺��1��������ɵã��ö��κ���ͼ��ĶԳ���Ϊֱ��x=-1��
�⣺��1��������ɵã��ö��κ���ͼ��ĶԳ���Ϊֱ��x=-1��
�ߵ�x=0ʱ��y=-4��
���C��������0��-4����
��S��ABC=
AB•|yC|=12��
��AB=6��
�֡ߵ�A��B����ֱ��x=-1�Գƣ�
��A���B�������ֱ�Ϊ��-4��0������2��0����
��4m+4m-4=0�����m=
��
��������κ����Ľ���ʽΪy=
x2+x-4��
��2����ͼ����DF��x���ڵ�F�������������
����������P��ֱ��AD���·�ʱ����ͼ��ʾ��
�ɣ�1���õ�A��-4��0������D��-2��1����
��DF=1��AF=2��
��Rt��ADF�У���AFD=90�㣬��tan��ADF=
=2��
�ӳ�DF�������߽��ڵ�P1����P1��Ϊ����
���P1��������-2��-4����
����������P��ֱ��AD���Ϸ�ʱ���ӳ�P1A����Gʹ��AG=AP1������DG����GH��x���ڵ�H����ͼ��ʾ��
��֤��GHA�ա�P1FA��
��HA=AF��GH=P1F��GA=P1A��
�֡�A��-4��0����P1��-2��-4����
���G�������ǣ�-6��4����
�ڡ�ADP1�У�
DA=
��DP1=5��
AP1=2
��
��DA2+AP12=DP12
���DAP1=90�㣮
��DA��GP1��
��DG=DP1��
���ADG=��ADP1��
��tan��ADG=tan��ADP1=2��
��DG�������ߵĽ���ΪP2����P2��Ϊ����
��DK��GH�ڵ�K����P2S��GK��DK�ڵ�S��
��P2���������x��
x2+x-4����
��P2S=
x2+x-4-1=
x2+x-5��DS=-2-x��
��
=
��GK=3��DK=4����
=
��
��������2x2+7x-14=0��
���x=
��
��P2���ڵڶ����ޣ�
��P2��ĺ�����Ϊx=
����������
���ϣ�P��ĺ�����Ϊ-2��
��
��3����ͼ������OO�䣬��CE��T������CO�䣮
�ߵ�O���CO�����EC����ֱ�߶Գƣ�
��OO���CE����OCE=��O��CE����CO��E=��COE=90�㣬
O��C��O��E��
��ON��O��E��
��O��C��ON��
���OMC=��O��CE=��OCE��
��OC=OM��
��CT=MT��
����Rt��ETO�У���ETO=90�㣬cos��OEC=
��
��Rt��COE�У���COE=90�㣬cos��OEC=
��
��
=
��
��OE2=ET•EC
=��EM+TM��•EC
=EM•EC+TM•EC
=48+TM•EC��
ͬ��OC2=CT•EC=TM•EC=16��
��OE2=48+16=64��
��OE��0��
��OE=8��
�ߵ�E��x����������ϣ�
��E���������8��0����
 �⣺��1��������ɵã��ö��κ���ͼ��ĶԳ���Ϊֱ��x=-1��
�⣺��1��������ɵã��ö��κ���ͼ��ĶԳ���Ϊֱ��x=-1���ߵ�x=0ʱ��y=-4��
���C��������0��-4����
��S��ABC=
| 1 |
| 2 |
��AB=6��
�֡ߵ�A��B����ֱ��x=-1�Գƣ�
��A���B�������ֱ�Ϊ��-4��0������2��0����
��4m+4m-4=0�����m=
| 1 |
| 2 |
��������κ����Ľ���ʽΪy=
| 1 |
| 2 |
��2����ͼ����DF��x���ڵ�F�������������
����������P��ֱ��AD���·�ʱ����ͼ��ʾ��
�ɣ�1���õ�A��-4��0������D��-2��1����
��DF=1��AF=2��
��Rt��ADF�У���AFD=90�㣬��tan��ADF=
| AF |
| DF |
�ӳ�DF�������߽��ڵ�P1����P1��Ϊ����
���P1��������-2��-4����
����������P��ֱ��AD���Ϸ�ʱ���ӳ�P1A����Gʹ��AG=AP1������DG����GH��x���ڵ�H����ͼ��ʾ��
��֤��GHA�ա�P1FA��
��HA=AF��GH=P1F��GA=P1A��
�֡�A��-4��0����P1��-2��-4����
���G�������ǣ�-6��4����
�ڡ�ADP1�У�
DA=
| 5 |
AP1=2
| 5 |
��DA2+AP12=DP12
���DAP1=90�㣮
��DA��GP1��
��DG=DP1��
���ADG=��ADP1��
��tan��ADG=tan��ADP1=2��
��DG�������ߵĽ���ΪP2����P2��Ϊ����
��DK��GH�ڵ�K����P2S��GK��DK�ڵ�S��
��P2���������x��
| 1 |
| 2 |
��P2S=
| 1 |
| 2 |
| 1 |
| 2 |
��
| P2S |
| GK |
| DS |
| DK |
| ||
| 3 |
| -2-x |
| 4 |
��������2x2+7x-14=0��
���x=
-7��
| ||
| 4 |
��P2���ڵڶ����ޣ�
��P2��ĺ�����Ϊx=
-7-
| ||
| 4 |
���ϣ�P��ĺ�����Ϊ-2��
-7-
| ||
| 4 |
��3����ͼ������OO�䣬��CE��T������CO�䣮
�ߵ�O���CO�����EC����ֱ�߶Գƣ�
��OO���CE����OCE=��O��CE����CO��E=��COE=90�㣬
O��C��O��E��
��ON��O��E��
��O��C��ON��
���OMC=��O��CE=��OCE��
��OC=OM��
��CT=MT��
����Rt��ETO�У���ETO=90�㣬cos��OEC=
| ET |
| OE |
��Rt��COE�У���COE=90�㣬cos��OEC=
| OE |
| EC |
��
| OE |
| EC |
| ET |
| OE |
��OE2=ET•EC
=��EM+TM��•EC
=EM•EC+TM•EC
=48+TM•EC��
ͬ��OC2=CT•EC=TM•EC=16��
��OE2=48+16=64��
��OE��0��
��OE=8��
�ߵ�E��x����������ϣ�
��E���������8��0����
���������⿼���˶��κ����ۺ��⣬�漰��֪ʶ���У��Գ������깫ʽ���������ϵ�����������������������ʽ������ϵ����������κ����Ľ���ʽ������˼�룬���Ǻ������ۺ��Խ�ǿ����һ�����Ѷȣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��ͼ����ƽ���ı���ABCD�У�EΪCD��һ�㣬����AE��BE��BD����AE��BD���ڵ�F��S��DEF��S��EBF��S��ABF=9��21��49����DE��EC=��������
��ͼ����ƽ���ı���ABCD�У�EΪCD��һ�㣬����AE��BE��BD����AE��BD���ڵ�F��S��DEF��S��EBF��S��ABF=9��21��49����DE��EC=��������| A��2��3 | B��2��5 |
| C��3��4 | D��3��7 |
����1��2��3�ķ�����ڣ�������
| A��1 | ||
| B��2 | ||
C��
| ||
D��
|
��2��1��0��-1���ĸ����У�С��0�����ǣ�������
| A��0 | B��-1 | C��1 | D��2 |
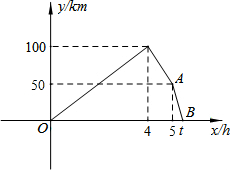 �ס�������ͬʱ��M�س������Ը��Ե��ٶ�������N����ʻ���׳��ȵ���N�أ�ͣ��1h��ԭ·��ԭ�����ٷ��أ�ֱ�������������ҳ����ٶ�Ϊ50km/h����ͼ������֮��ľ���y��km�����ҳ���ʻʱ��x��h��֮��ĺ���ͼ��
�ס�������ͬʱ��M�س������Ը��Ե��ٶ�������N����ʻ���׳��ȵ���N�أ�ͣ��1h��ԭ·��ԭ�����ٷ��أ�ֱ�������������ҳ����ٶ�Ϊ50km/h����ͼ������֮��ľ���y��km�����ҳ���ʻʱ��x��h��֮��ĺ���ͼ��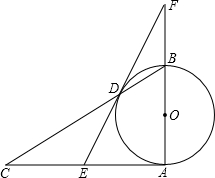 ��֪����ͼ����Rt��ABC�У���A=90�㣬��ABΪֱ������O��BC����O�ڵ�D��E�DZ�AC���е㣬ED��AB���ӳ����ཻ�ڵ�F��
��֪����ͼ����Rt��ABC�У���A=90�㣬��ABΪֱ������O��BC����O�ڵ�D��E�DZ�AC���е㣬ED��AB���ӳ����ཻ�ڵ�F��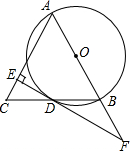 ��ͼ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC=BD������AC������D��EF��AC������ΪE����AB���ӳ����ڵ�F��
��ͼ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC=BD������AC������D��EF��AC������ΪE����AB���ӳ����ڵ�F��