题目内容
已知:关于x的一元二次方程(k2-1)x2-(3k-1)x+2=0.
(1)当方程有两个相等的实数根时,求k的值;
(2)若k是整数,且关于x的一元二次方程(k2-1)x2-(3k-1)x+2=0有两个不相等的整数根时,把抛物线y=(k2-1)x2-(3k-1)x+2向右平移
个单位长度,求平移后抛物线的顶点坐标.
(1)当方程有两个相等的实数根时,求k的值;
(2)若k是整数,且关于x的一元二次方程(k2-1)x2-(3k-1)x+2=0有两个不相等的整数根时,把抛物线y=(k2-1)x2-(3k-1)x+2向右平移
| 1 |
| 2 |
考点:根的判别式,二次函数图象与几何变换
专题:计算题
分析:(1)根据一元二次方程的定义和判别式的意义得到k2-1≠0且△=(3k-1)2-4×2×(k2-1)=0,然后解不等式和方程得到k的值为3;
(2)利用公式法解方程得到x1=
,x2=
,由于方程有两个不相等的整数根,且k≠±1,则整数k=0,于是抛物线解析式表示为y=-x2+x+2,配方得到y=-(x-
)2+
,即抛物线的顶点坐标为(
,
),然后根据点的坐标变换求解.
(2)利用公式法解方程得到x1=
| 2 |
| k+1 |
| 1 |
| k-1 |
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
解答:解:(1)根据题意得k2-1≠0且△=(3k-1)2-4×2×(k2-1)=0,
解得k=3,
所以k=3时,原方程有两个相等的实数根;
(2)∵△=(3k-1)2-4×2×(k2-1)=(k-3)2,
∴x=
,
∴x1=
,x2=
,
∵方程有两个不相等的整数根,且k≠±1,
∴整数k=0,
当k=0时,抛物线为y=-x2+x+2=-(x-
)2+
,
∴抛物线的顶点坐标为(
,
),
∴把抛物线y=-x2+x+2向右平移
个单位长度后,得到的抛物线的顶点坐标为(1,
).
解得k=3,
所以k=3时,原方程有两个相等的实数根;
(2)∵△=(3k-1)2-4×2×(k2-1)=(k-3)2,
∴x=
| 3k-1±(k-3) |
| 2(k2-1) |
∴x1=
| 2 |
| k+1 |
| 1 |
| k-1 |
∵方程有两个不相等的整数根,且k≠±1,
∴整数k=0,
当k=0时,抛物线为y=-x2+x+2=-(x-
| 1 |
| 2 |
| 9 |
| 4 |
∴抛物线的顶点坐标为(
| 1 |
| 2 |
| 9 |
| 4 |
∴把抛物线y=-x2+x+2向右平移
| 1 |
| 2 |
| 9 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了二次函数图象与几何变换.

练习册系列答案
相关题目
已知点A(2,y1)和点B(m,y2)是抛物线y=x2-2x上两点,且y2>y1,则m的取值范围是( )
| A、m>2 |
| B、m≤0或m≥2 |
| C、0<m<2 |
| D、m<0或m>2 |
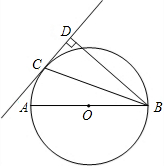 如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.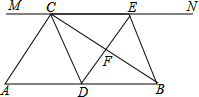 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
 如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是
如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是