题目内容
16. 如图,在平面直角坐标系中,四边形OABC是矩形,OA=16cm,OC=8$\sqrt{2}$cm,两动点M、N分别从O、C同时出发,M在线段OA上沿OA方向以每秒2cm的速度匀速运动,N在线段CO上沿CO方向以每秒$\sqrt{2}$cm的速度匀速运动,设运动时间为t秒(0≤t≤8).
如图,在平面直角坐标系中,四边形OABC是矩形,OA=16cm,OC=8$\sqrt{2}$cm,两动点M、N分别从O、C同时出发,M在线段OA上沿OA方向以每秒2cm的速度匀速运动,N在线段CO上沿CO方向以每秒$\sqrt{2}$cm的速度匀速运动,设运动时间为t秒(0≤t≤8).(1)求△OMN的面积的最大值;
(2)四边形OMBN的面积是一个定值吗?若是,求出定值;若不是,请说明理由;
(3)当△OMN与△ABM和△MBN都相似时,抛物线y=$\frac{1}{4}$x2+bx+c经过B、M两点,过线段BM上一动点P作x轴的垂线交抛物线于点Q,交NB于点H,当线段PQ的长取得最大值时,求△PBH的面积.
分析 (1)用t表示OM、ON,根据S△OMN=$\frac{1}{2}$ON•OM,构建二次函数,利用配方法求最大值.
(2)根据S四边形OMBN=S矩形OABC-S△BCN-S△ABM计算即可.
(3)根据待定系数法可得抛物线解析式为y=$\frac{1}{4}$x2+($\sqrt{2}-6$)x+32-8$\sqrt{2}$,设P(t,$\sqrt{2}$t-8$\sqrt{2}$),则Q(t,$\frac{1}{4}$t2+($\sqrt{2}$-6)t+32-8$\sqrt{2}$),H(t,$\frac{\sqrt{2}}{4}$t+4$\sqrt{2}$),构建二次函数,即可解决问题.
解答 解:(1)∵OM=2t,CN=$\sqrt{2}$t,ON=8$\sqrt{2}$-$\sqrt{2}$t=$\sqrt{2}$(8-t),
∴S△OMN=$\frac{1}{2}$ON•OM=$\frac{1}{2}$×2t×$\sqrt{2}$(8-t)=-$\sqrt{2}$t2+8$\sqrt{2}$t=-$\sqrt{2}$(t-4)2+16$\sqrt{2}$(0≤t≤8),
∵a=-$\sqrt{2}$<0,
∴当t=4时,S△OMN取最大值16$\sqrt{2}$.
(2)是一个定值.理由如下:
∵S四边形OMBN=S矩形OABC-S△BCN-S△ABM=OA•OC-$\frac{1}{2}$BC•CN-$\frac{1}{2}$AB•AM=16×8$\sqrt{2}$-$\frac{1}{2}$×16×$\sqrt{2}$t-$\frac{1}{2}$×8$\sqrt{2}$×(16-2t)=64$\sqrt{2}$,
∴四边形OMBN的面积是一个定值,该定值为64$\sqrt{2}$.
(3)当△OMN与△ABM与△MBN相似时,△BMN必须是直角三角形,
∴∠BMN=90°
∴△OMN∽△ABM∽△MBN,
∴$\frac{MO}{AB}$=$\frac{ON}{MA}$,即$\frac{2t}{8\sqrt{2}}$=$\frac{8\sqrt{2}-\sqrt{2}t}{16-2t}$,解得t=4或8(舍弃),
∴OM=8.ON=4$\sqrt{2}$,
∴M(8,0),N(0,4$\sqrt{2}$)
设直线BM解析式为y=kx+b,则有$\left\{\begin{array}{l}{16k+b=8\sqrt{2}}\\{4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\sqrt{2}}\\{b=-8\sqrt{2}}\end{array}\right.$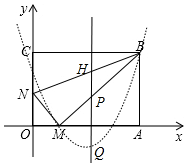
∴直线BM的解析式为y=$\sqrt{2}$x-8$\sqrt{2}$,
设直线BN的解析式为y=mx+n,则有$\left\{\begin{array}{l}{n=4\sqrt{2}}\\{16m+n=8\sqrt{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{\sqrt{2}}{4}}\\{n=4\sqrt{2}}\end{array}\right.$
∴直线BN的解析式为y=$\frac{\sqrt{2}}{4}$x+4$\sqrt{2}$,
∵抛物线的解析式y=$\frac{1}{4}$x2+bx+c经过B(16,8$\sqrt{2}$),M(8,0),
则有$\left\{\begin{array}{l}{64+16b+c=8\sqrt{2}}\\{16+8b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=\sqrt{2}-6}\\{c=32-8\sqrt{2}}\end{array}\right.$,
∴y=$\frac{1}{4}$x2+($\sqrt{2}-6$)x+32-8$\sqrt{2}$,设P(t,$\sqrt{2}$t-8$\sqrt{2}$),
则Q(t,$\frac{1}{4}$t2+($\sqrt{2}$-6)t+32-8$\sqrt{2}$),H(t,$\frac{\sqrt{2}}{4}$t+4$\sqrt{2}$)
∴PQ=$\sqrt{2}$t-8$\sqrt{2}$-($\frac{1}{4}$t2+($\sqrt{2}$-6)t+32-8$\sqrt{2}$=-$\frac{1}{4}$t2+6t-32=-$\frac{1}{4}$(t-12)2+4,
∴当t=12时,PQ最大值是4,此时P(12,4$\sqrt{2}$),H(12,7$\sqrt{2}$),
∴S△PBH=$\frac{1}{2}$×$4×3\sqrt{2}$=6$\sqrt{2}$.
点评 本题考查二次函数的综合题、一次函数、多边形面积问题.最值问题等知识,解题的关键是灵活运用待定系数法确定函数解析式,学会构建二次函数解决最值问题,属于中考压轴题.

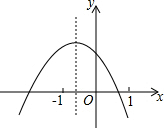 二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)
二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)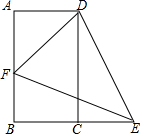 已知,如图,矩形ABCD,点E是线段BC延长线上一点,且AB=BE,F为边AB上一点,∠DEF=45°.
已知,如图,矩形ABCD,点E是线段BC延长线上一点,且AB=BE,F为边AB上一点,∠DEF=45°.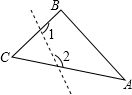 如图,在△ABC中,∠C=40°,若沿图中虚线剪去∠C,则∠1+∠2=120°.
如图,在△ABC中,∠C=40°,若沿图中虚线剪去∠C,则∠1+∠2=120°. 已知a,b,c在数轴上的对应点如图所示,化简|a|-|a+b|+|c-a|+|b+c|.
已知a,b,c在数轴上的对应点如图所示,化简|a|-|a+b|+|c-a|+|b+c|.